土木学会論文集G Vol.64 No.1, 46-61, 2008. 2 スクラップタイヤを用いた地中振動遮断壁の提案とその振動低減効果の評価
| 正会員 |
中谷 郁夫 立命館大学大学院 総合理工学研究科(〒525-8577 草津市野路東1-1-1) |
|---|---|
| フェロー会員 |
早川 清 立命館大学 理工学部 環境システム工学科(〒525-8577草津市野路東1-1-1) |
|
樫本 孝彦 株式会社 オーク(〒668-0024 兵庫県豊岡市寿町8番30号) |
|
|
西村 忠典 株式会社 構造計画研究所(〒164-0011 東京都中野区中央4-5-3) |
地盤振動問題にスクラップタイヤを用いた新たな地中振動遮断壁について検討するために,原形のタイヤを用いた原形型遮断壁とタイヤを圧縮配置した圧縮型遮断壁について,実物大の遮断壁を実フィールドに埋設した.実際の振動源を想定した加振実験を実施して,この遮断壁による振動低減効果を観測した.その結果,原形型遮断壁では3dB~4dB,圧縮型遮断壁では5dB~12dBの効果量を確認した.また,遮断壁による振動低減効果の評価に関して,波動透過理論による評価値にタイヤゴムのバネ効果に関する検討を加えて実測値と比較した.この評価法により実測値をほぼ再現できたことから,提案の遮断壁による振動低減効果は,波動の透過効果とタイヤのバネ効果の2つの効果の相互作用で評価できることが判明した.
-
はじめに
近年の循環型経済社会の構築を背景に,リサイクルへの取り組みが活発に行われている.これは,資源の再資源化であるが,再使用はもちろん発生抑制も含めたもので,生態系を維持する環境保全が目的とされている.工業の分野では,電化製品,自動車において有効な再生利用の研究が進められている.また,建築・建設の分野では,主に建設副産物である発生土,コンクリート塊,アスファルトコンクリート等が,建設資材としてリサイクルされている1).自動車部品の一部であるタイヤは,わが国の自動車産業の発展に伴い,タイヤの生産量が年々増加しており,年間に約1億8000万本,質量にして約120万トンとなっている.タイヤの交換時等のスクラップタイヤの発生量も生産量に比例して増加しており,ここ数年の年間発生量は,約1億300万本,質量で約103万トンである2),3).スクラップタイヤの概ね9割は,リサイクルされている.その内訳は,約4割がサーマルリサイクル(燃料利用),約3割が海外輸出であり,その中でリユース(再使用)やマテリアルリサイクル(原料利用)は,約2.5割である.この値は,欧米諸国と比較して低く,サーマルリサイクルの比率が大きい.その燃焼によってCO2が発生するために,地球温暖化への影響が懸念される.したがって,この分野での再利用の促進が急務の課題となっている.土木分野でのスクラップタイヤの一般的な有効利用は,弾性舗装,アスファルトラバーとしてのリユースである4).また,最近では,地盤材料として,固化処理土にタイヤチップを混入した場合に,粘り強い靭性を有する材料特性を示すことが知られており,強度特性が低下しない軽量な地盤材料や地震時土圧の緩衝材などとしての研究4),5)が進められており,さらなるスクラップタイヤのリサイクルが期待されている.
一方,著者らは,以前から地盤環境振動問題(以下:地盤振動)を解決するために,幾つかの地中振動遮断壁(以下:遮断壁)について検討している.都市部での土地利用の高過密度化や渋滞緩和対策としての高架橋形式による鉄道網や道路網が輻輳して建設整備されたこと,鉄道車両の軌道走行量および自動車の走行量と走行速度の増加も,地盤振動の発生要因の1つである.また,建設現場の建設機械,工場の大型機械などによって生じる振動も,地盤振動を引き起こす原因と成っている.こうした問題を解決するために,既往の地盤振動対策法としては,発振源側・伝播経路側・受振部側における対策がある.この中でも,施工時に交通機関などの供用を阻害することなく対策が可能な方法としての,伝播経路における対策法の1 つには,遮断壁が挙げられる.この対策法に着目すると,剛性壁では,コンクリート壁,鋼矢板および地盤改良などによる方法6)がある.また,最近では,ガスクッション,発泡スチロール,発泡ウレタンなど軟らかい材料と先に述べた剛な材料とを組み合わせたハイブリット構造が提案されている.例えば発泡スチロールとコンクリート壁を組み合わせた遮断壁7),ガスクッションと鋼矢板を組み合わせた遮断壁8),9)などが提案されている.これらは,地盤に対しての波動インピーダンス(波動速度×密度)比が単一材料に比べて大きく得られることに,振動低減効果を期待したものである.
本論文では,新たな遮断壁としてのスクラップタイヤの軟らかい材料特性に着目している.材料特性とCO2の削減対策に加えてその費用対効果にも着目しており,このような研究事例はほとんど見られない.中心部を剛な材料で構成したものを提案し,その振動低減効果を検討している.従来の幾つかの遮断壁は,材料コストが高くなる点や循環型経済社会の構築を重視していないことに課題があった.この点を解決するために,スクラップタイヤを使用することでコストを低減し,リユースやリサイクル率を上げることが可能であると考えられる.本研究では,遮断壁の振動低減効果を検討するために2つの実験を実施した.第1実験では,原型のタイヤを利用したスクラップタイヤ原形型地中振動遮断壁(以下:原形型遮断壁)に関する実物大フィールド実験を行い,第2実験では,タイヤの原型を鉛直方向に圧縮したスクラップタイヤ圧縮型地中振動遮断壁(以下:圧縮型遮断壁)に関する実物大フィールド実験を行った.遮断壁の振動低減効果を評価するために第1実験と第2 実験を比較して,この対策法の振動低減効果について評価・検討した.また,振動低減効果の評価をさらに検討するために,三次元モデルを用いたFEM シュミレーション解析を実施し,解析値と実測値を比較して振動低減効果を考察している.
-
実物大実験の目的と方法
本研究の実験では,実際現場に使用した場合での振動低減効果の基礎資料を得るために,実物大フィールド実験を実施した.スクラップタイヤを原形のまま使用してその中空部(元の使用時では空気が充填されていた部分)および中心部(タイヤホイルが装着されていた部分)を空隙とした2005年の実験では,振動低減効果への有効性が確認10)されている.今回の実験では,より実現場への適用に近い条件とするために,タイヤの中心部および中空部を充填した実験を行った.これは,中空にしても地下水の浸入が考えられることおよび現地発生土の有効処理を目的としたものである.
第1実験では,スクラップタイヤを原形のまま使用して,先に述べた実験のタイヤ中空部にはタイヤシュレッズ(スクラップタイヤ破砕片)およびコンクリートを充填し,中心部には砂質土を充填したものである.また,第2実験では,鋼管杭およびPHC杭を芯材にしてその周辺にタイヤを鉛直方向に圧縮配置し,杭の中心部を砂質土により充填したものである.これらの実験結果から振動低減特性を比較し,この遮断壁を用いた地盤振動対策の有効性を立証しようとしたものである.
-
第1実物大実験
本実験では,兵庫県豊岡市内の建設会社の敷地に原形型遮断壁を埋設した.写真-1は,その状況を示したもので,使用したスクラップタイヤは普通自動車用である.その形状寸法を図-1に示す.外径φ60cm,内径φ40cmで,中空部10cmの外側5cmにはタイヤシュレッズを充填して内側5cmにはコンクリートを充填した.埋設深さはGL-6.0m,施工延長はL=10.0mで,中心部を砂質土で充填している.また,施工延長方向の遮断壁ごとの接続は突合せによるものである.遮断壁の埋設配置の詳細は,3.(4)の図-3に示した.


-
地盤状況
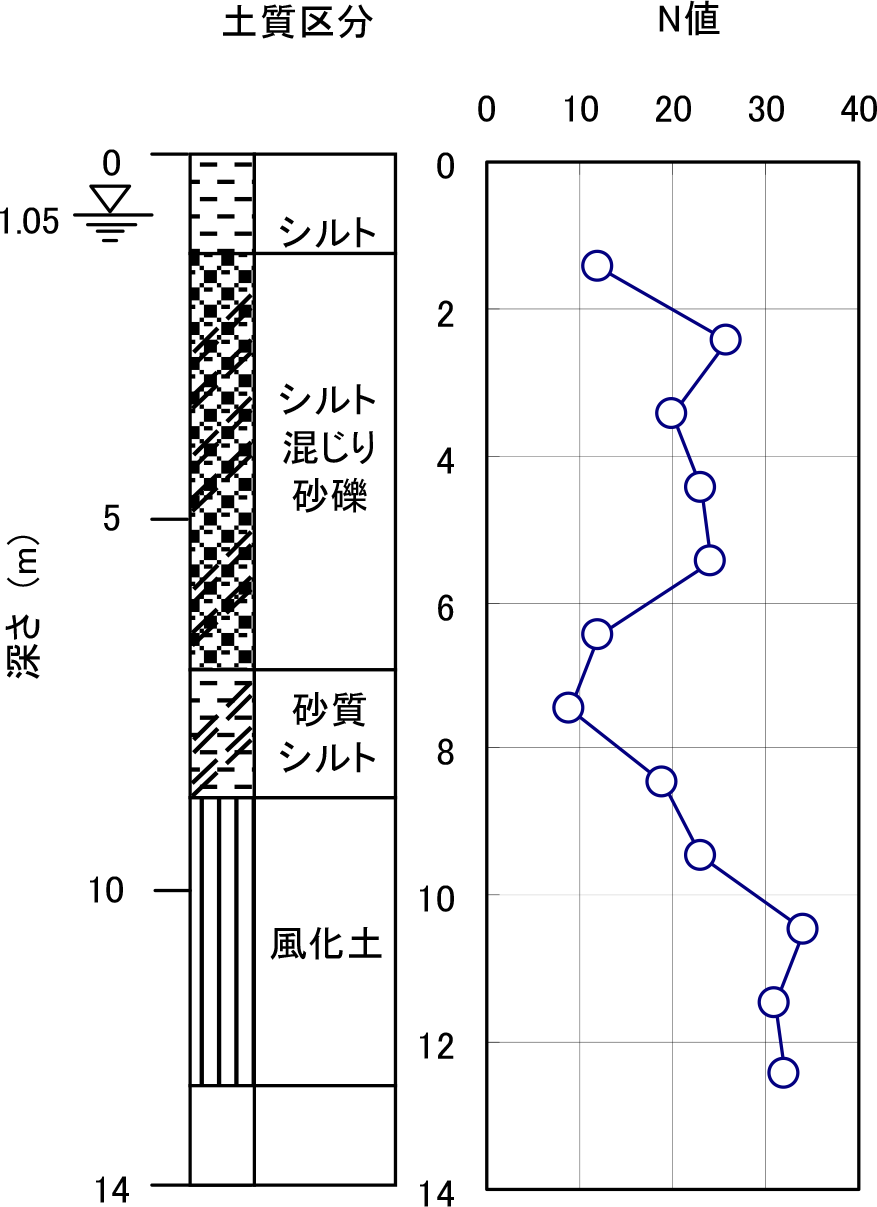
実験フィールドの地盤状況は,ボーリング調査より地表面からGL-8.4mまではシルト混じり砂礫および砂質シルトで構成され,平均N値が18程度である.それ以深はN値が30程度である.図-2にボーリング柱状図を示す.地盤のせん断波速度(VS)を今井他による地盤を砂質土とした推定式(1)11)から求めると,上層はVS=210m/sec,下層はVS=249m/secと推定される.
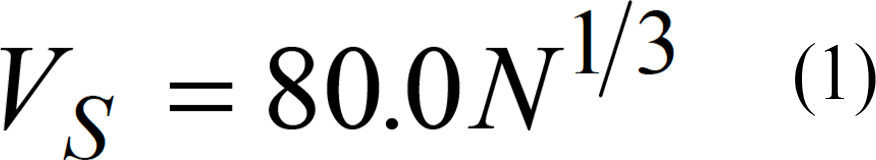
ここに,
VS:せん断波速度(m/sec)
N:地盤のN値 -
加振方法
地盤振動問題となる振動源は,車両などの段差走行などで発生する衝撃的な振動と,車両などの走行面との摩擦によって発生する定常的な振動が主要である.このような特徴を再現する方法として,本実験では加振方法を2水準とした.衝撃加振は重錘を用いて行った.その形状寸法は,先端が平らな円柱形で,φ36cm×高さ100cmの鋼管に砂を充填したものである.重量が約3.0kNの重錘を地表面から0.5mの高さから自由落下させる重錘落下法を用いた.重錘の吊り上げおよび自由落下は,250kNのラフタークレーンを用いて行った.また,定常加振としては,重機を走行させて行った.使用した重機は0.5m3級のバックホウで,遮断壁の打設延長方向と平行に走行させて加振している.
-
計測配置と計測機械
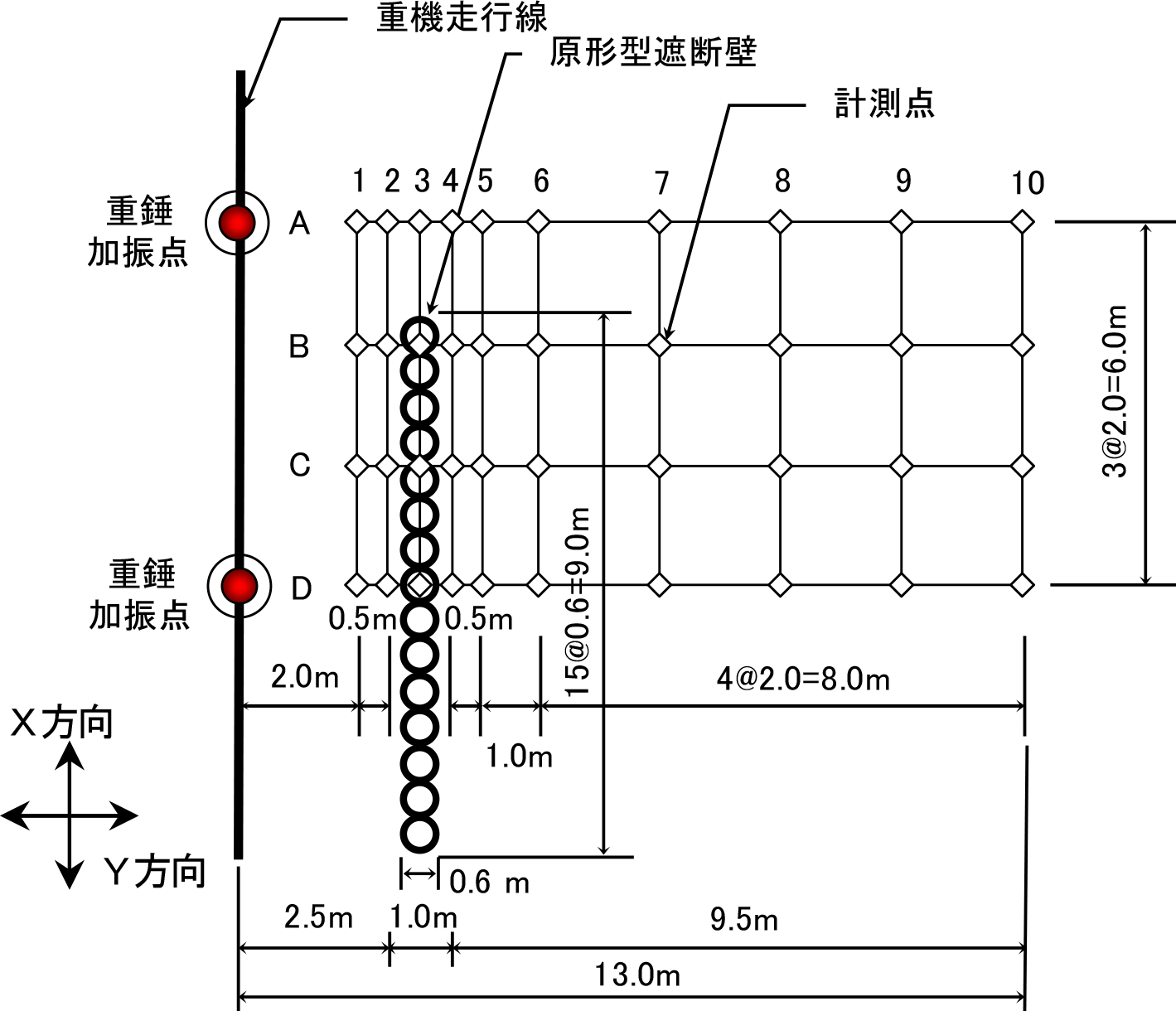
図-3は,地表面での計測配置を示したものである.遮断壁の無いAラインから遮断壁中心線のDラインまでの4測線を設定して,1測線当たり10点の計40測点を配置した.計測領域は縦幅6.0m×横幅13.0mの区域を設定し,計測点は遮断壁の前面と背後の計測番号1から5では0.5m間隔で,測点5から6では1.0m間隔とし,それ以降の6から10では2.0m間隔とした.地表面の計測では,5台の3成分計測可能なピックアップおよび5台のポータブル振動計(リオン(株)製VM‐52)を使用して,振動加速度レベルの上下成分(Z方向)を計測した.また,遮断壁の上部とその前面と背後の3点の水平直角成分(Y方向)および上下成分(Z方向)を同時記録するために,3台のピックアップおよびポータブル振動計にデータレコーダ(ティアック電子計測(株)製LX‐10)を接続して加速度波形を収録し,遮断壁の前面と背後および遮断壁上部の動的挙動を確認した.
-
計測条件
地表面での計測は,図-3に示す遮断壁の中心Dラインおよび無対策自然地盤でのAラインの延長線上の位置で,遮断壁中心から3.0m地点に重錘を用いて衝撃加振を行い,そのときに発生した波動の振動加速度レベルの最大値をメータの指示値で計測するとともに,同時にデータレコーダへの波形記録も行った.Dラインの加振入力では,30測点(3ライン×10測点)を1ケース当り3回実施しており,Aラインでは10測点(1ライン×10測点)を1ケース当り3回実施している.また,定常加振では衝撃加振と同様に,遮断壁中心から3.0m地点が重機の中心線となるように走行させた.Aライン~Dラインでの40測点(4ライン×10測点)で,1ケース当り2回の計測を行っている.重錘加振では,全部で24回程度落下させて実験を実施した.この際,重錘落下により地表面が凸凹となり,地表面の地盤が締め固まることによる振動入力の再現性の損なわれることが懸念された.しかしながら,加振点から2m(計測点1)の地点での3回の重錘落下ごとの振動レベルが同一値になることを確認しており,一定の振動が入力できたことを確認している.
-
振動低減挙動
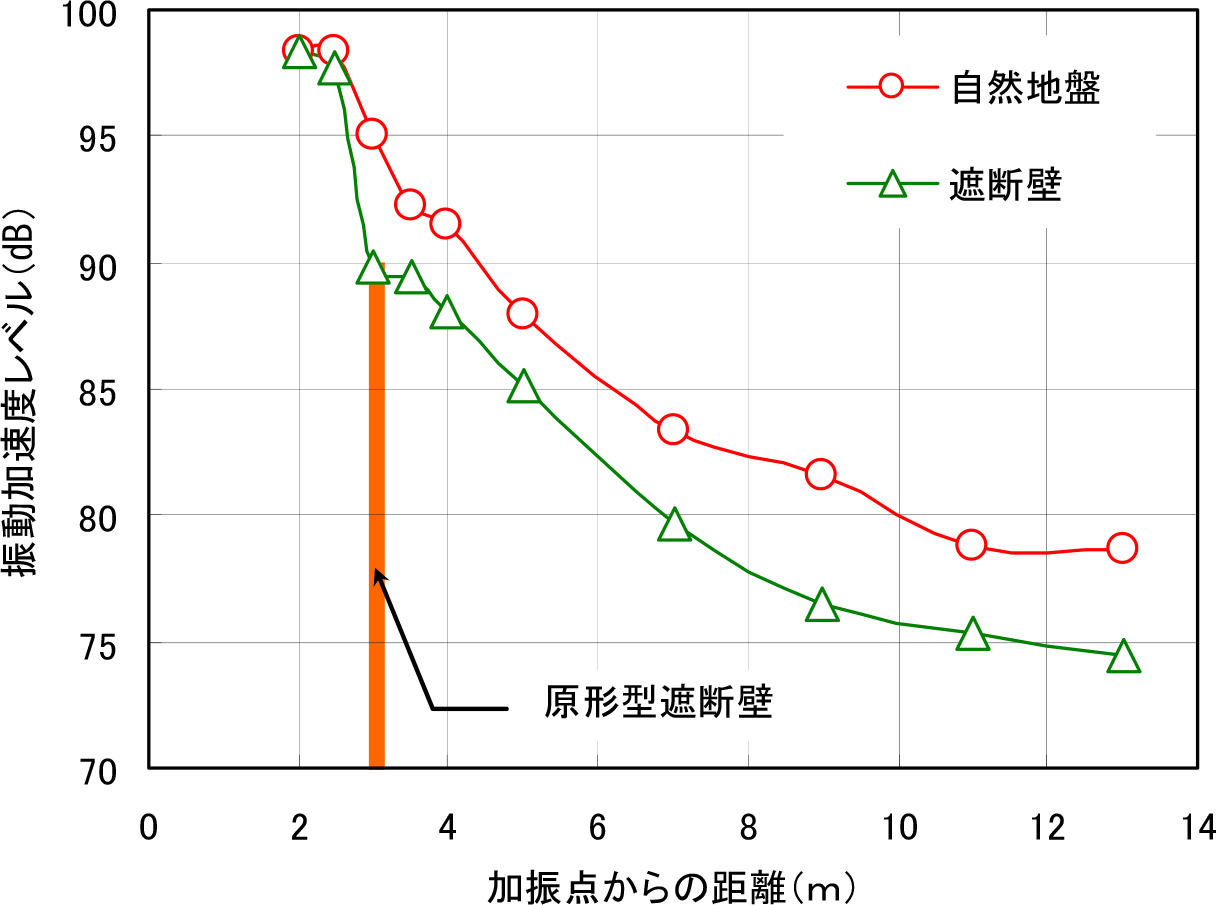
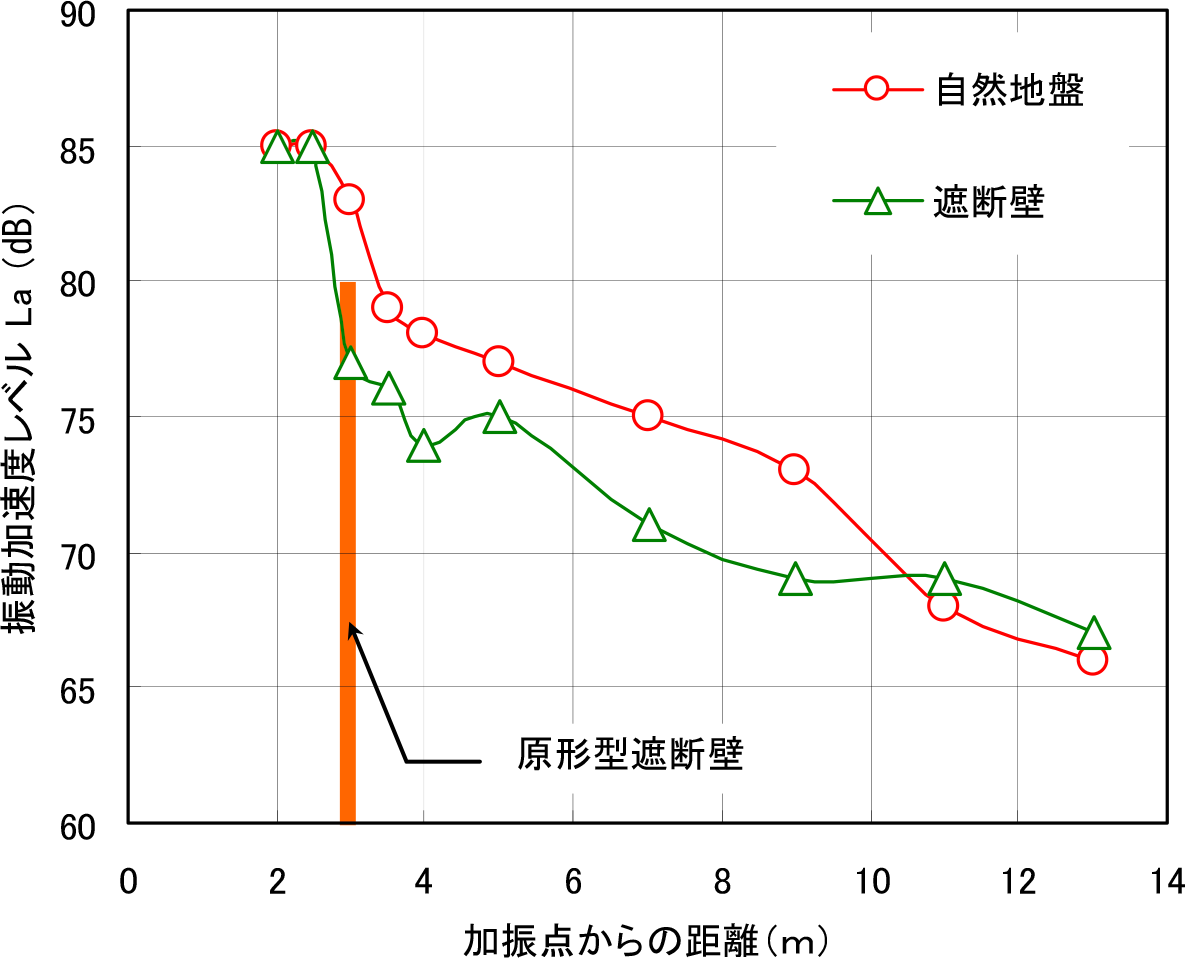
図-4は,重錘加振による地表面における振動低減挙動を示したものである.また図-5には,重機加振による代表的な結果を示している.これらのデータは,遮断壁の中心線であるDラインと自然地盤であるAラインの鉛直方向の値(Z方向)を,それぞれ振動加速度レベルで比較している.重錘加振では,遮断壁の背後では自然地盤に比べて3dBから4dB程度の振動低減量を示している.また,重機加振においても,遮断壁の背後以降においては3dBから4dB程度の振動低減量を示していることが分かる.加振水準による違いを見ると,重機加振での加振点から10m地点以降においては,自然地盤の値とほぼ同様である.このことは,重機走行においては振動が連続的に発生していることから,遮断壁端部から回り込んだ波動による回折現象の影響と考えられる.以下では,遮断壁の周波数領域における振動挙動について検討している.この目的から,Dラインの結果について考察した.また,このような遮断壁の振動挙動が振動低減効果の低下に与える影響は水平方向成分によるものがより大きいと考えられるので,ここでは水平成分のみについて検討している.
-
重錘加振による加速度スペクトル
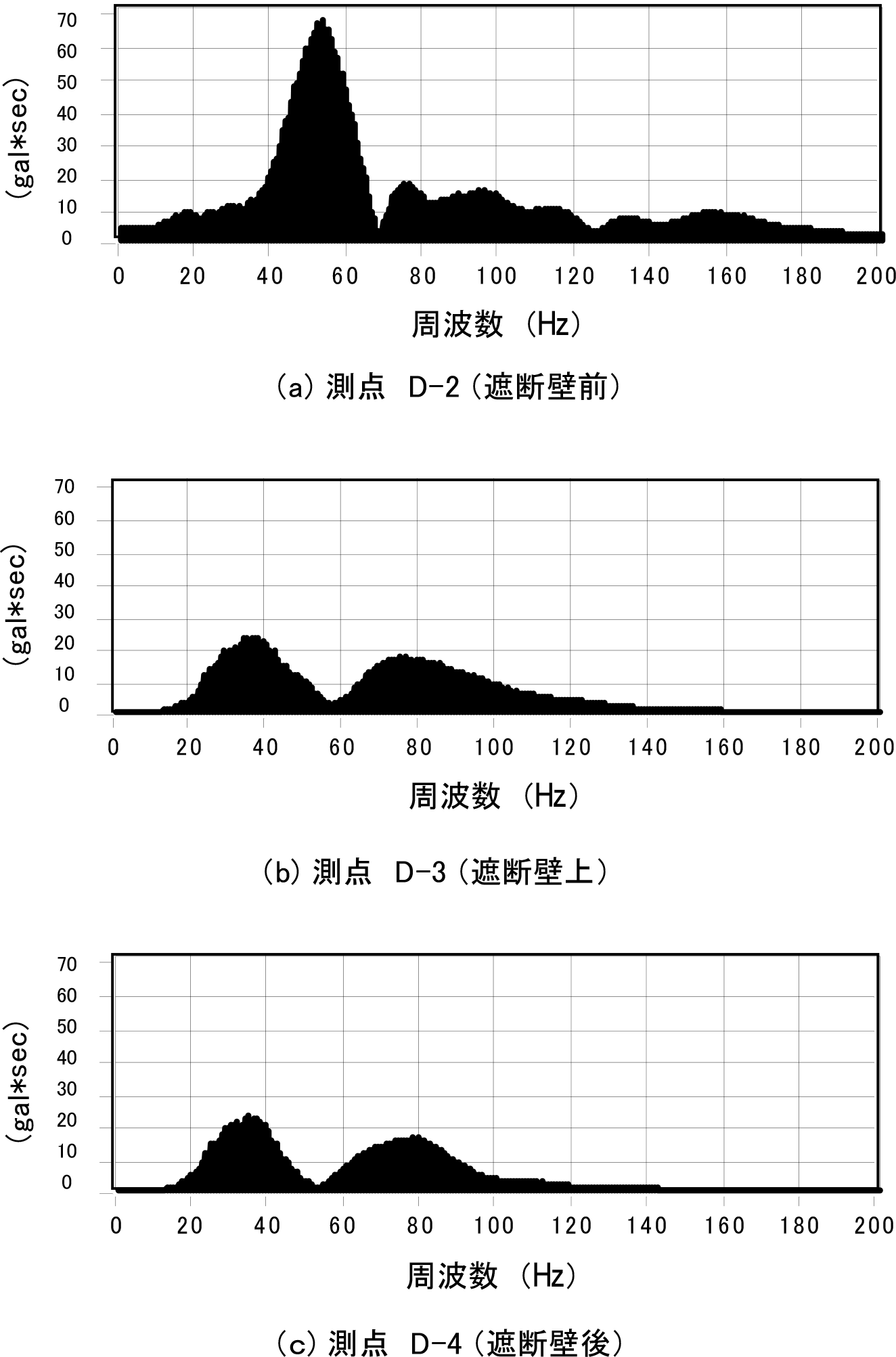
図-6は,重錘加振による加速度記録のフーリエスペクトルを示したものである.加振点からの距離が2.5m地点の遮断壁前面の測点(D-2),3.0m地点の遮断壁上の測点(D-3)および遮断壁背後の測点(D-4)における遮断壁の水平直角方向の記録を処理したものである.遮断壁前面の地盤では,50Hz付近の振動数が卓越していることから,この値が重錘の自然落下による地盤の応答周波数であることが分かる.また,遮断壁上部および遮断壁背後では,遮断壁前面と比較して50Hz付近の周波数成分が減衰し,40Hz付近が卓越していることが分かる.したがって,この現象から知られるように,特に顕著な遮断壁の振動低減効果は40Hzから60Hz付近で得られていることが推定される.
このような振動低減効果は,タイヤ部分によるものとコンクリート部分によるものとの相互影響によるものと考えられる.このことに関する考察は,5章に示す第1実験および第2実験を比較した振動低減効果の評価から検討している.
-
重機加振による加速度スペクトル
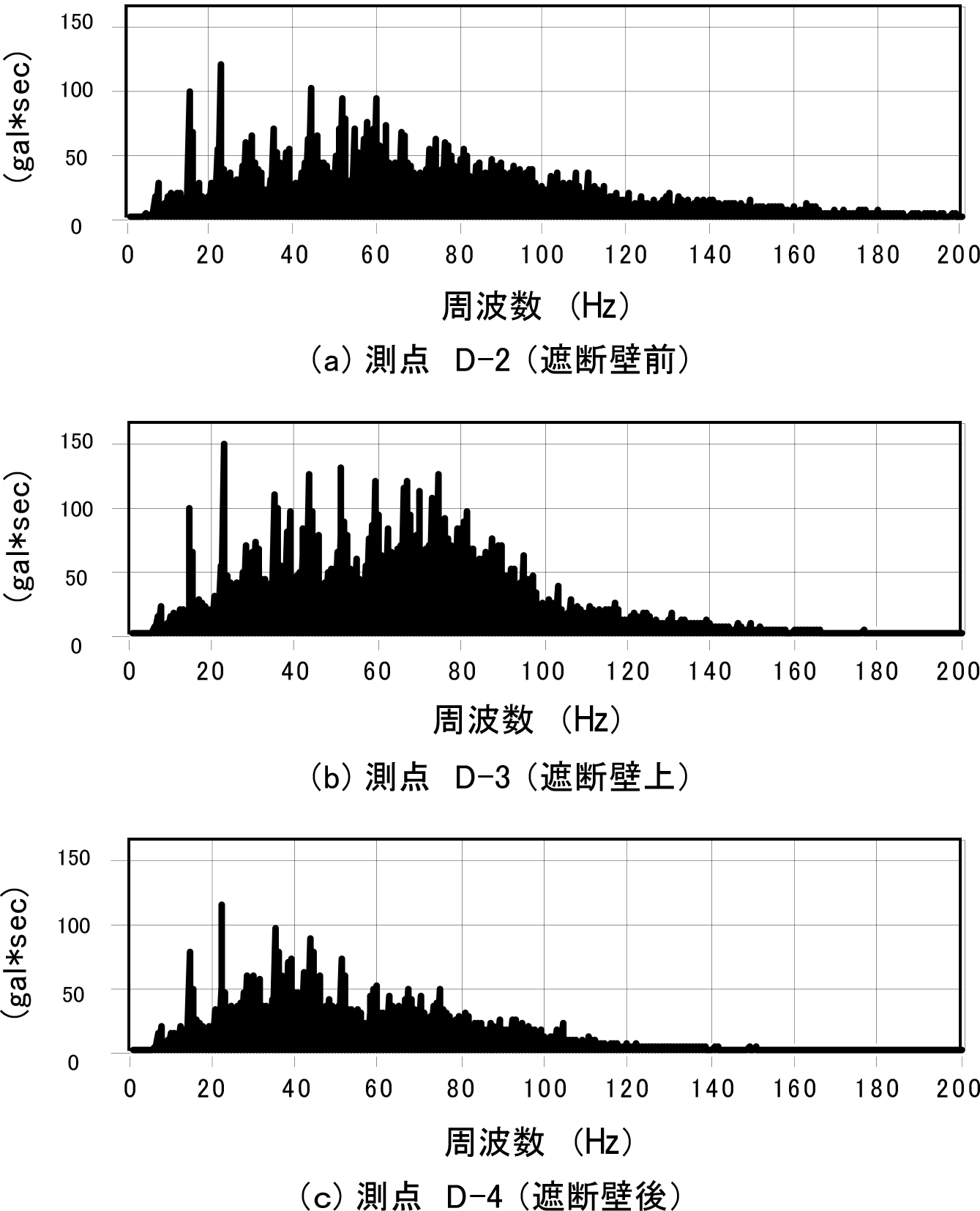
図-7は,重機加振における加速度記録のフーリエスペクトルを示したもので,測点は前節(6)と同様の測点である遮断壁の前面と背後,およびその上部での水平直角成分の記録である.遮断壁前面の測点では,15Hz,22Hz,2Hz,50Hzおよび60Hz付近の多くの周波数成分が卓越していることが分かる.また,前節(6)の重錘落下実験での結果に比べて卓越周波数成分がばらついているが,これは重機の走行する地盤面が均一な平滑面でないために,重機の各部位と地盤との応答により複数の周波数成分が発生されたためと思われる.遮断壁の上部では,遮断壁前面の卓越成分にさらに遮断壁独自の動的挙動のために65Hz,75Hzを付加した高い周波数成分が卓越している.この帯域の振動数成分は距離減衰が大きいので,遮断壁による振動低減対策としては余り問題にならないと考えられる.また,遮断壁の背後では,15Hz,22Hzおよび42Hzの周波数成分が卓越しており,45Hz~75Hzの遮断壁上部で卓越していた周波数成分が大きく減衰されている.この傾向は,前節(6)で述べたものと同様な傾向を示している.重錘加振による結果との違いは,遮断壁上部での振動応答にある.これは,重機加振では連続的に波動が伝播されることにより,遮断壁が水平方向にも運動したものと考えられる.これらのことより,原形型遮断壁では,特に45Hz~75Hzの周波数域での遮断効果の大きいことが示唆される.

-
発生波動の検討
図-8は,前節(6)の重錘加振と同じ計測点での地表面分布の鉛直方向(Z方向)と水平直角方向(Y方向)での同時記録により,質点の代表的な運動軌跡を示したもので,遮断壁前面の地盤→遮断壁→遮断壁背後の地盤に伝わる波動伝播特性の変化を見たものである.また,鉛直方向に加振力が加わった場合の波動エネルギーは,レイリー波が最も強く全エネルギーの65%を占め,横波が26%,縦波が7%と最も小さいこと12)が知られている.したがって,地盤の振動問題では,まずレイリー波が問題となる事例が多い.表面波であるレイリー波は,Z方向とY方向との振動に位相差が生じるため,波動の進行方向に対して反時計回りの回転運動軌跡を描くことが知られている13).本実験での遮断壁前面の測点(D-2)では,はじめに逆回転運動を行いその後時計周りの順回転運動を示している.順回転運動を行うのは,(ア)基本的なレイリー波の波動伝播方向と異なり,上下動の加速度が水平動の加速度より大きくなること.(イ)遮断壁前面での波動の反射により軌跡の向きが時計回りになるためと考えられる.遮断壁上部の測点(D-3)および遮断壁背後の測点(D-4)では逆回転運動となっていることから,遮断壁を透過した波動が単純なレイリー波の特性を示すものと考えられる.地表分布における水平直角方向(Y方向)の振動加速度の変化は,遮断壁前の測点(D-2)での60galの値が遮断壁上部の測点(D-3)では50galに変化し,遮断壁背後の測点(D-4)では40galを示す.これより,遮断壁の前面と上部では約0.8倍に減衰し,上部と背後においても約0.8倍に減衰していることが分かる.次に鉛直方向(Z方向)の振動加速度の変化では,遮断壁前面の測点(D-2)での120galの値が遮断壁上部の測点(D-3)では50galに変化し,遮断壁背後の測点(D-4)では30galを示している.これより,遮断壁の前面と上部では約0.4倍に減衰し,上部と背後においても約0.6倍に減衰している.したがって,鉛直方向(Z方向)の方が水平直角方向(Y方向)と比較しての減衰の大きいことが分かる.これらのことから理解されることは,原形型遮断壁の振動低減効果は,遮断壁前面での波動の反射と透過量の減少による鉛直方向(Z方向)成分の振動低減効果によるものと考えられる.
-
-
第2実物大実験
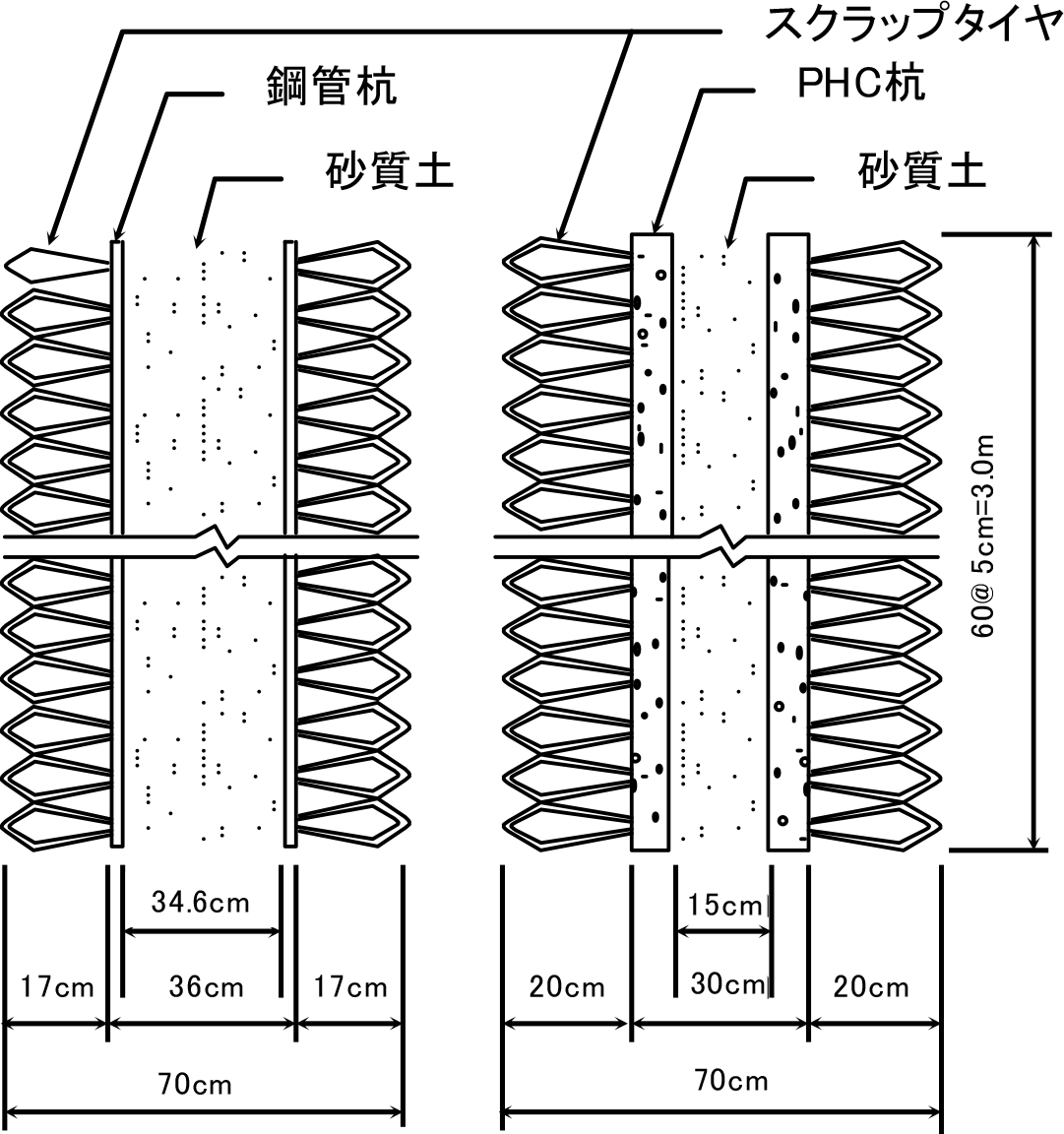
第1実験では,原形のスクラップタイヤを利用して,中空部にタイヤシュレッズとコンクリートを充填した原形型遮断壁を用いた実験を行った.第2実物大実験では,写真-2に示すスクラップタイヤの中心部に鋼管杭およびPHC杭を配置して,タイヤを鉛直方向に圧縮して取り付けた構造を用いて検討している.この目的は,タイヤのばね定数の低下による振動遮断性能の向上を期待するとともに,スクラップタイヤのリサイクル率が上がるものと考えたからである.それらの形状寸法を図-9に示す.中心部の芯材が鋼管杭(以下:鋼管Type)では,遮断壁は長さL=3.0mで,タイヤ外径φ70cm,中心杭の外径φ36cm,内径φ34.6cmである.また,中心部の芯材がPHC杭(以下:PHC Type)の場合では,遮断壁は長さL=3.0mで,タイヤ外径φ70cm,中心杭の外径φ30cm,内径φ15cmである.第1実験では,1本の遮断壁の1m当りにタイヤを5本使用したが,第2実験では,第1実験の4倍の20本のタイヤを使用している.芯材に鋼管杭およびPHC杭を用いた理由は,5.章で考察しているようにインピーダンス比の増加を期待したものである.実験地は,兵庫県豊岡市内の市が所有する土地を借地している.2水準の圧縮型遮断壁を埋設して,その埋設深さは深さ3m以下のN値30以上の支持層により遮断壁の下部が固定されるものと考えて,GL-3.0mとしている.図-10の計測配置の詳細に示すように,遮断壁の施工延長および施工配置は,芯材が鋼管杭ではL型に配置して9.8m+3.5mの計13.3mで,芯材がPHC杭では同様にL型で9.8m+3.5mの計13.3mの2水準の遮断壁を埋設している.それぞれの遮断壁の中心部には,現場で掘削時に発生した砂質土を充填している.また,圧縮型遮断壁の隣合うピースの接合は,緊結せずに突合わせて地中に埋設している.

-
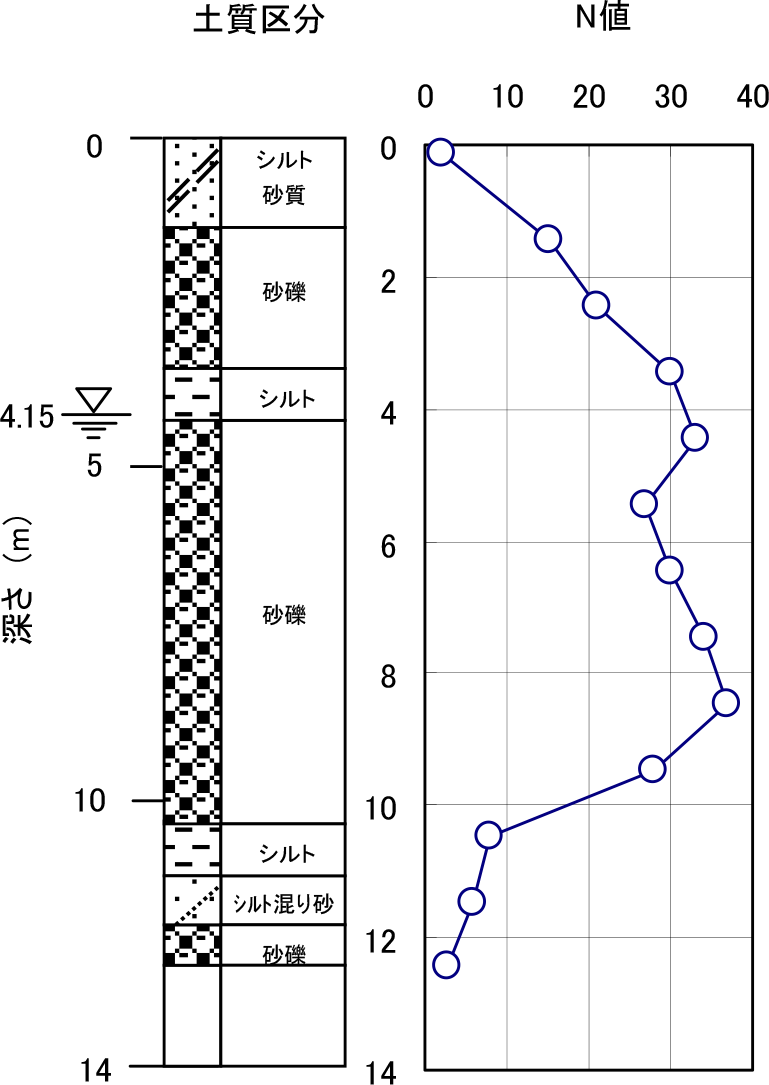
地盤状況
第2実験におけるフィールドの地盤条件を図-11に示す.ボーリング調査より,地表面からGL-4.0mまではシルト混じり砂質土および砂礫,シルトで構成され,N値が2から30程度で平均N値が17である,それ以深のGL-4.0mからGL-10.0mまでは砂礫層でN値が30程度,それ以深ではN値が8程度である.また,実験場周辺公共工事に伴って調査されたボーリング調査では,N値が50以上に達するのはGL-22.0m以深であることが分かっている.地盤のせん断速度(VS),推定式(1)から上層部のN値を17とするとVS=206m/secで,下層部のN値を30とするとVS=249m/secと推定される.
-
加振方法と計測配置および計測機械
第1実験での加振方法は,衝撃的な振動源としての重錘による自由落下法によるものと,定常的な振動としての重機走行による2水準の方法とした.その波形記録から分析した加速度記録のフーリエスペクトルによると,重錘加振では重機加振と比較して一定の振動数が卓越していること,また,基本的な振動低減効果が得られる周波数帯域は,重錘加振およおび重機加振ともにほぼ同程度であることが第1実験で分かった.そのために,第2実験では,重錘による自由落下法を採用して振動低減効果を検討している.第1実験と同様な方法を用いて,重量約3.0kNの重錘を第1実験よりも落下高さを0.5m増加した高さh=1.0mから自由落下させて加振している.これは,より実現場に近い広範囲までの伝播状況を確認するために,第1実験よりも計測配置を遮断壁後方へと測定距離を長くしているためである.
第2の実物大実験の計測配置図を図-10に示し.圧縮型遮断壁の埋設状況を写真-3に示す.中心部芯材がPHC杭および鋼管杭の2水準を同じフィールドに同時に埋設している.計測領域は,幅34.0m×長さ19.5m=663m2に配置している.測線は,A~Rの18ラインとして1測線当り13点の測点を配置し,全234点で計測している.計測間隔は,測点1から3を1.0m間隔とし,遮断壁を挟む3から5では0.75m間隔で,5から7では1.0mとして,その後方の測点7から13は2.0m間隔としている.また,本報告では省略しているが,遮断壁の配置は,隅角部の振動低減効果を確認するためにL型配置としている.
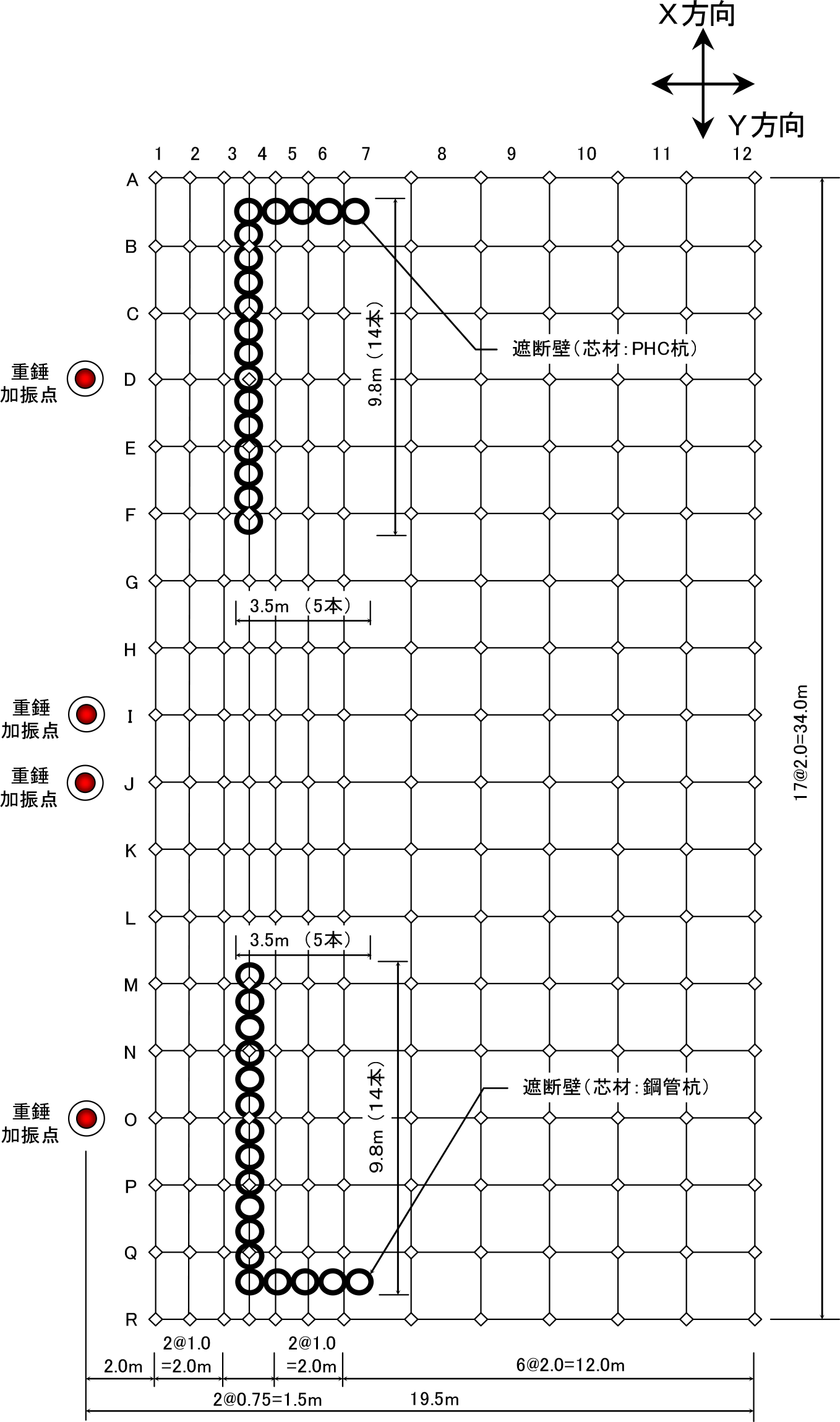
計測機械は,地表面の計測では第1実験と同様に5台のポータブル振動計(リオン(株)製VM-52)を使用して,振動加速度レベルの上下成分(Z方向)を計測した.また,遮断壁の上部およびその前面と背後では,水平直角成分(Y方向)5点と上下成分(Z方向)5点を同時に計測するために,5台のピックアップおよび5台のポータブル振動計にデータレコーダ(ティアック電子計測(株)製LX-10)を接続して加速度波形を収録し,遮断壁周辺の地盤の挙動および圧縮型遮断壁の挙動を確認した.
-
計測条件
第2実験での地表面の計測は,第1実験と同様にポータブル振動計を5台同時に使用して計測を行った.図-10に示すように,芯材がPHC杭遮断壁の中心Dライン,鋼管杭遮断壁の中心Oライン,無対策な自然地盤のPHC杭側のIラインおよび鋼管杭側のJラインの延長線上の,遮断壁中心線から4.75m地点に重錘を用いて衝撃加振を行い,そのときに発生した振動加速度レベルの最大値を計測した.また,同時に加速度波形を記録している.DラインおよびOラインの加振では,それぞれの91測点(7ライン×13測点)での計測を1ケース当り3回実施して,無対策の自然地盤であるIラインおよびJラインでは,それぞれ13測点(1ライン×13測点)を1ケース当り3回計測している.重錘加振は,遮断壁の芯材別に2水準について55回程度重錘を落下させて実施している.重錘落下により地表面が凸凹となるために落下毎に地表面をしき均し,地表面における振動応答が一定となるようにして計測を行った.
-
振動低減挙動
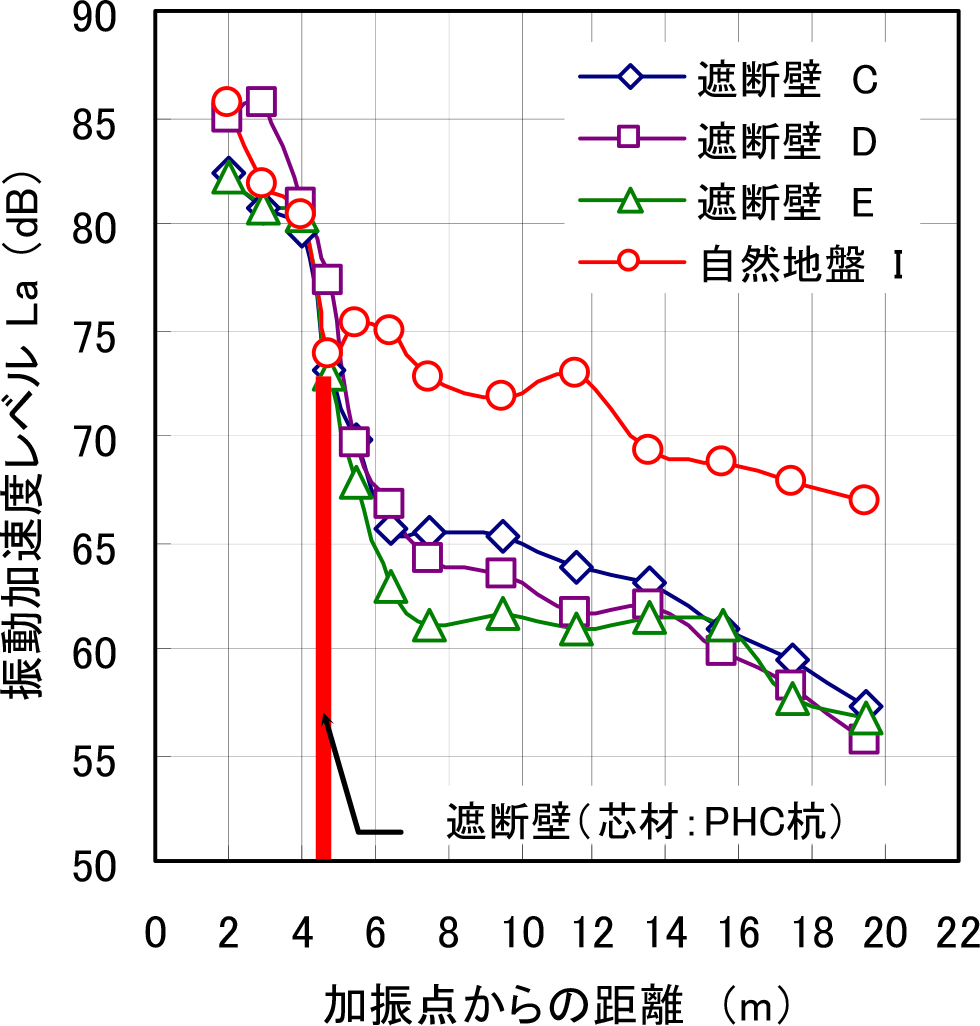
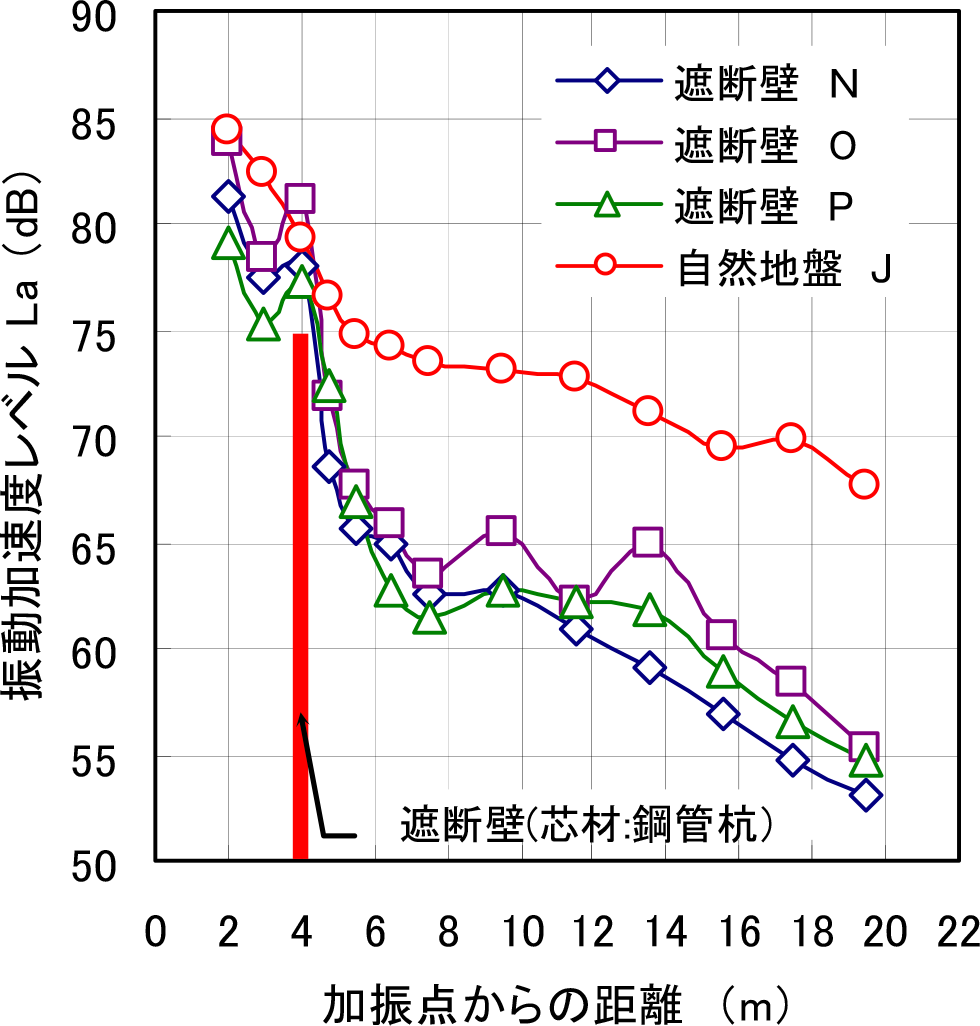
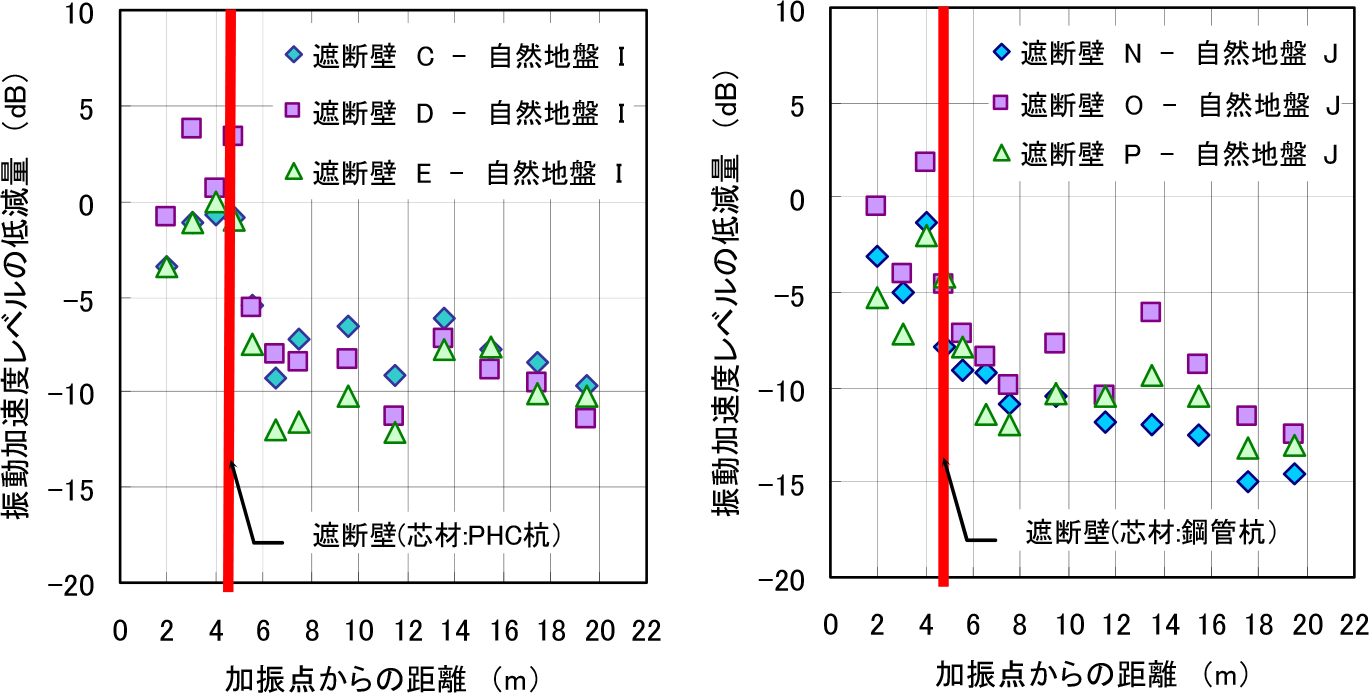
図-12は圧縮型遮断壁の芯材がPHC Typeの場合の,図-13は遮断壁の芯材が鋼管Typeの場合の,地表面における振動低減挙動の代表例を示したものである.図-12では,遮断壁の中心線であるDラインと,その隣り合うCラインとEラインを遮断壁による対策データとして,Iラインを無対策の自然地盤として振動低減効果を比較している.同様に図-13は,遮断壁の中心線であるOラインと,その隣り合うNラインとPラインを遮断壁による対策データとして,Jラインを無対策の自然地盤として振動低減効果を比較している.両タイプともに加振点から4.75m地点にある遮断壁を境にして,大きな振動低減効果が生じている.PHC Typeの遮断壁では,加振点から4.75m~14.0mではほぼ一定の振動加速度レベルを示しており,14.0m以降では自然地盤の距離減衰と同様な傾きを示している.また鋼管Typeの遮断壁では,加振点から4.75m~12.0mではほぼ一定の振動加速度レベルを示し,12.0m以降では自然地盤の距離減衰と同様な傾きを示している.図-14は,両Typeの遮断壁と自然地盤とを比較して,振動加速度レベルの振動低減量をグラフ化したものである.このグラフから,PHC Typeの遮断壁では,遮断壁後方の加振点から4.75m~16.0m地点では,自然地盤と比較して5dB~10dB程度の振動低減量を示し,16.0m以降では10dB程度の振動低減量を示していることが分かる.また鋼管Typeの遮断壁では,遮断壁後方の加振点から4.75m~16.0m地点では,自然地盤と比較して7dB~12dB程度の振動低減量を示し16.0m以降では10dB~15dB程度の振動低減量を示すことが分かる.この結果から,振動遮断壁の中心部の芯材には鋼管杭を用いた方が,振動遮断効果が大きく得られる傾向にあることが確認出来た.別途に,砂を充填したPHC杭のみの遮断壁による実験を行っており,PHC Typeと比較して4dB程度低減効果が少なくなることを確認している.次節以降では,この遮断効果についての分析を行う.
-
発生波動の検討
図-15は,圧縮型遮断壁のPHC Type,鋼管Typeの2ケースにおける,重錘落下による地表面の振動軌跡を示したものである.計測は,計測ラインD(PHC Type)と計測ラインOの測点3から5である遮断壁の前面,上部,背後の水平直角成分(Y方向)と鉛直成分(Z方向)で行なっている.同時記録した加速度波形データを用いて振動軌跡を作成している.この軌跡より,遮断壁中心部の芯材の違いによる波動伝播特性を検討する.
上述したように,主として地表面を伝播する表面波のレイリー波の振動軌跡は,水平直角成分(Y方向)と鉛直成分(Z方向)に位相差が生じて,波動の進行方向に対して反時計回りの回転運動軌跡を示すことが分かっている13).遮断壁前面の軌跡では,両ケースの遮断壁ともに反時計回りの回転運動軌跡が示されており,重錘落下によりレイリー波の発生していることが確認できる.また,PHC Typeの遮断壁の上部(中心の砂質部)では,先に述べた前面での軌跡とさほど変化がなく,反時計回りの回転運動軌跡を示している.鋼管Type遮断壁の上部(中心の砂質部)では,順回転運動を示している.このことから,単純なレイリー波とは異なり,上下動の振幅が水平動の振幅より小さくなり,運動軌跡の向きが時計回りと同じになるためと考えられる14).また,PHC Typeに比べて水平直角成分(Y方向)と鉛直成分(Z方向)の両成分の減衰の大きいことが分かる.これは,図-12および図-13に示した遮断壁芯材の違いによる振動低減挙動の比較からも分かる.すなわち,鋼管Typeでは自然地盤と比較して遮断壁の前面で振動加速度レベルが一度低減して,その後,遮断壁の前面で増加している.また,PHC Typeでの遮断壁前面での振動低減傾向は,自然地盤とほぼ同様な傾向を示していることから,鋼管TypeはPHC Typeに比べて遮断壁前面での波動の反射量が大きいと考えられる.そのために,運動軌跡においても,鋼管Typeでの遮断壁上部の減衰が大きく観測されているものと考えられる.

-
加速度スペクトル
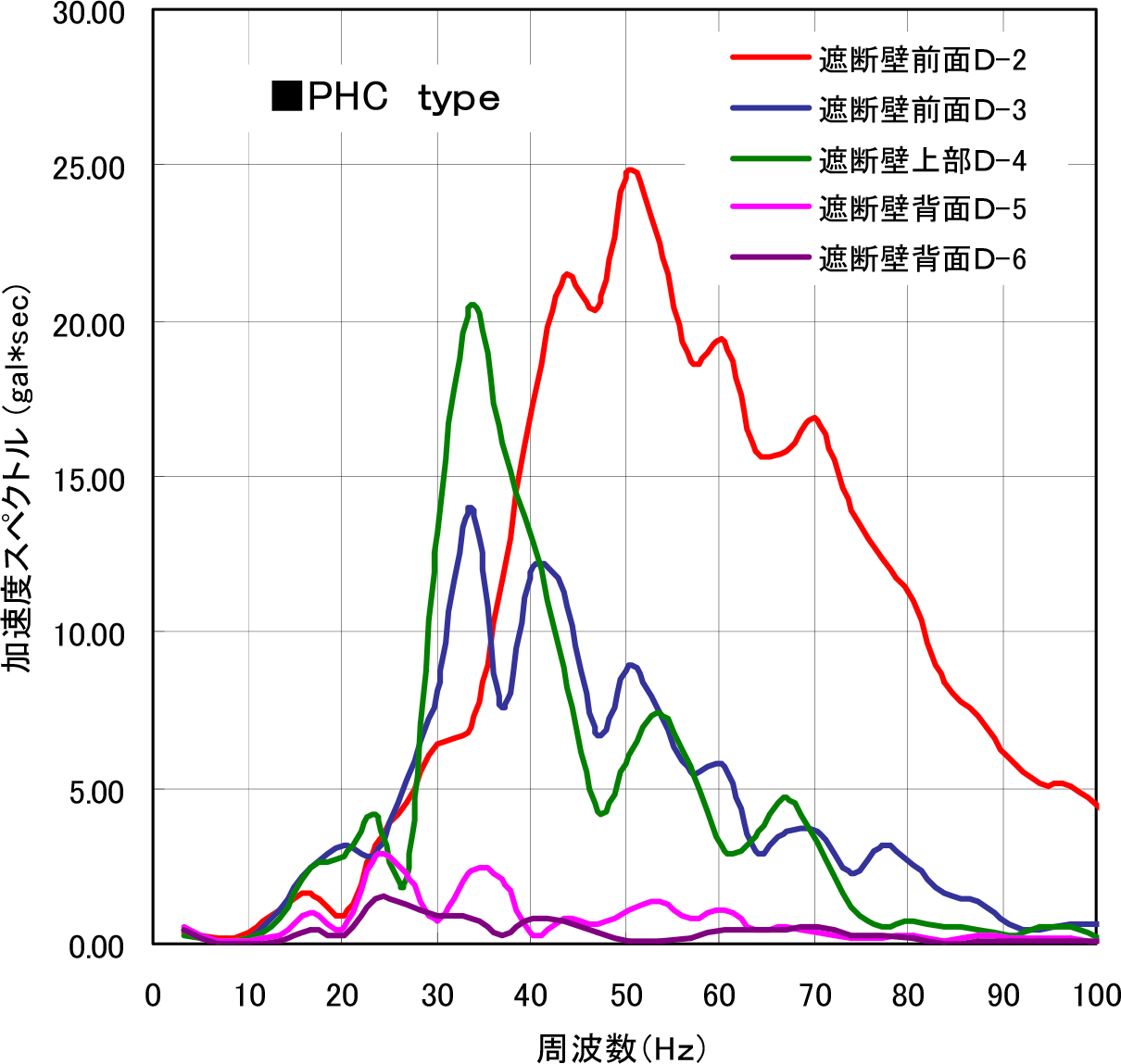
図-16,図-17は,PHC Typeおよび鋼管Typeの水平直角方向の加速度波形記録から求めた加速度スペクトルを,遮断壁前面の2測点,遮断壁上部の1測点および遮断壁背後の2測点に関して,加振点からの距離変化による周波数領域での振動低減効果を示したものである.
PHC Typeでは,遮断壁前面の測点(D-2)では50Hz付近,測点(D-3)では35Hz付近にピークがある.遮断壁上部の(D-4)においても35Hz付近のピークが優勢で,遮断壁前面よりも振幅が大きく増加している.このことより,この遮断壁の固有振動数は,35Hz付近にあると推察される.遮断壁背後の(D-5),(D-6)では,23Hz付近がピークである.これらから,遮断壁による振動低減効果は,23Hzから70Hz付近にあると考えられる.
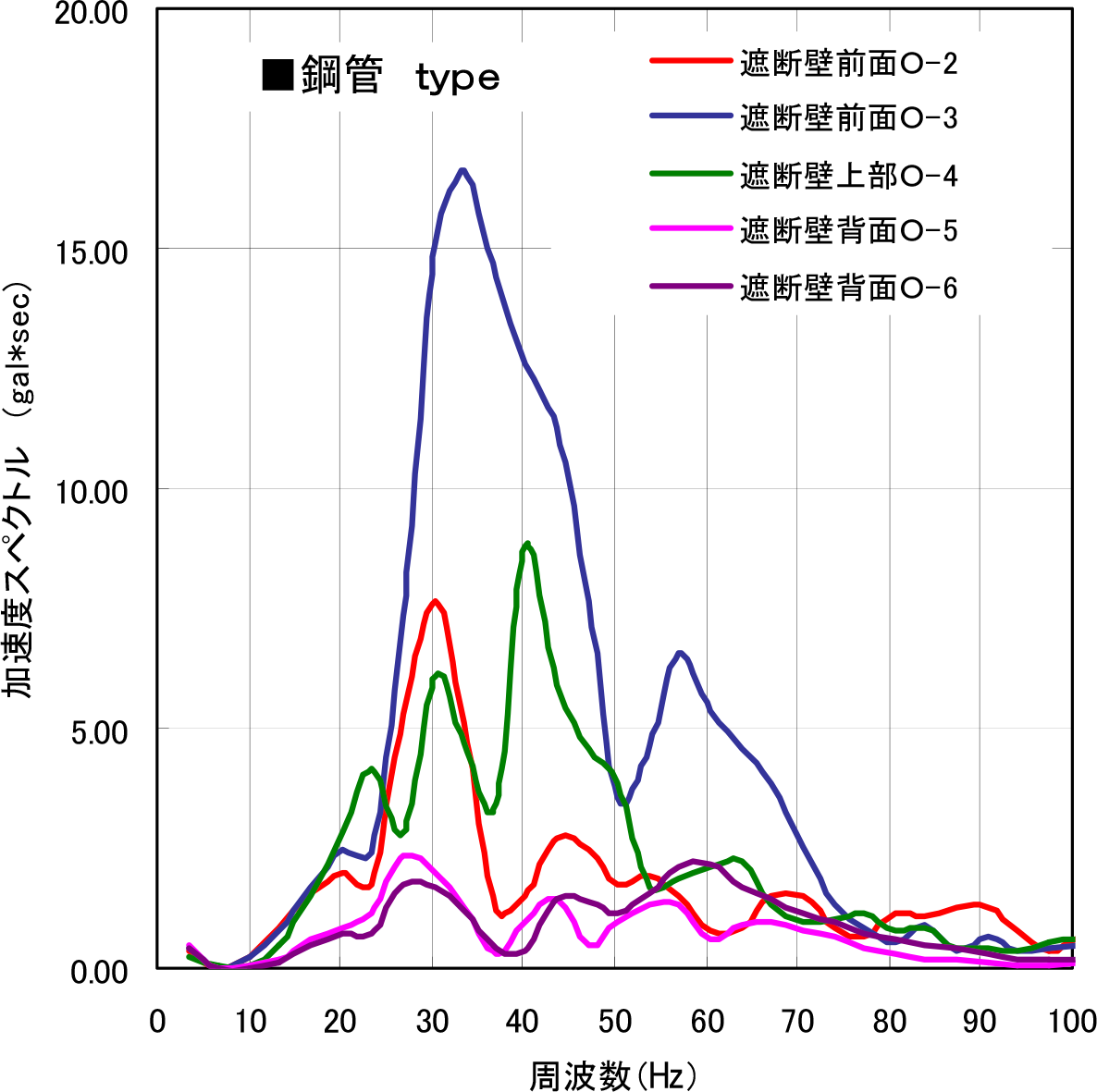
鋼管Typeでは,PHC Typeと同様に遮断壁前面の測点(O-2)では30Hz付近,(O-3)では33Hz付近にピークがある.遮断壁上部の(O-4)では,40Hz付近のピークが優勢である.遮断壁背後の(O-5),(O-6)では,26Hz付近がピークである.PHC Typeと同様に,遮断壁の振動低減効果は,23Hz以上から70Hz付近にあると考えられる.これらの結果から,重錘落下による両遮断壁の固有振動数は,30Hzから40Hz付近であることが理解される.
-
-
振動遮断効果に関する考察
-
第1実験と第2実験の振動低減効果の比較
図-18は,第1実験と第2実験の振動低減効果を比較して示したもので,加振条件は重錘自由落下法によるものである.この比較では,2ケースでの異なる地盤条件での結果を評価する方法を考察している.既往の研究成果から,応答振動数(f)をせん断波速度(VS)で除した波長(λ=VS/f)と遮断壁の埋設深さ(H)が振動低減効果に関係していることが分かっている.そこで,遮断壁の埋設深さを波長で除したR(H/λ)と振動遮断壁の前面と背後での加速度比(γ=a/a0)の関係を求めて,振動低減効果を評価している.また,同時に空溝の遮断効果とも比較するために,模型実験から求められている式(2)に示す実験式15)から求めた加速度比の値もプロットしている.
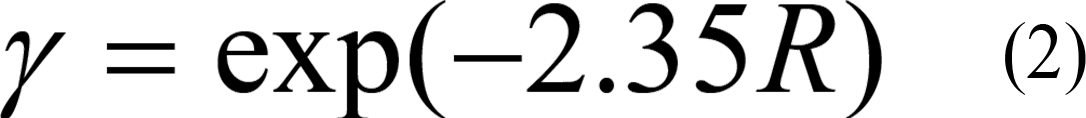
ここに,
γ :加速度比
R : H/λ 溝の深さと波長との比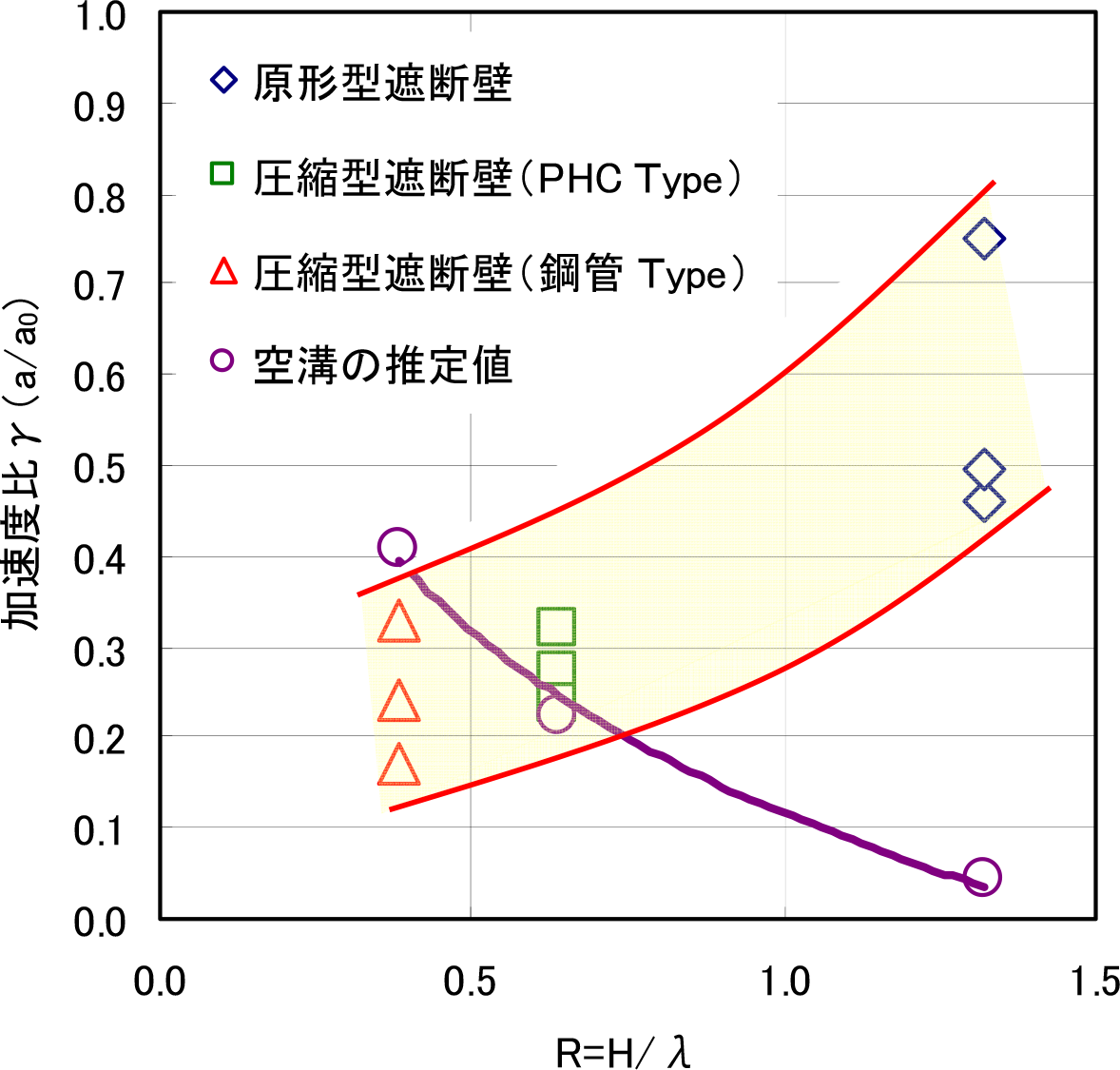
図-18から,第2実験における圧縮型遮断壁は,第1実験の遮断壁と比較してPHC Type,鋼管Typeともに大きな振動低減効果が得られていることが分かる.また,芯材の違いによる影響は,図-14から考察したものと同様に,鋼管TypeがPHC Typeに比較して若干大きな振動低減効果を示すことが理解される.さらに,第2実験と空溝による実験式から推定して求めた振動低減効果との比較では,PHC Type,鋼管Typeの両ケースともに空溝の振動低減効果に近似した値を示していることが理解される.したがって,原形タイヤを利用してタイヤシュレッズとコンクリートを充填したものよりも,既成杭にスクラップタイヤを圧縮して配置したものの方が,大きな振動低減効果の得られることが分かる.タイヤ部分の構造では,圧縮配置したスクラップタイヤの方が,原形タイヤにタイヤシュレッズを充填してコンクリートで成形したものよりもタイヤ部分の密度が小さくなり,柔らかい構造となる.したがって,ばね効果が得られるとともに,中心部の芯材料との波動インピーダンス比の相違が,振動低減効果に影響しているものと考えられる.以下の節では,振動低減効果についての理論的考察を行っている.
-
振動低減効果の検証
地中振動遮断壁による振動低減効果の評価法は,遮断壁に対する,入射波振幅と遮断壁を透過する振幅との比として,波動インピーダンス比をパラメータとした波動透過理論により評価される.インピーダンスは電気回路の特性を表すものであり,作用力に対する抵抗を表すもので,振動数の関数である速度振幅(電圧振幅)の力振幅(電流振幅)に対する比である.これに対して波動インピーダンスは,密度(ρ)と伝播速度(V)の積で定義される.波動透過理論によれば,地中振動遮断壁に入射した波動とその媒質を透過した加速度振幅の比は,式(3)で表現される.
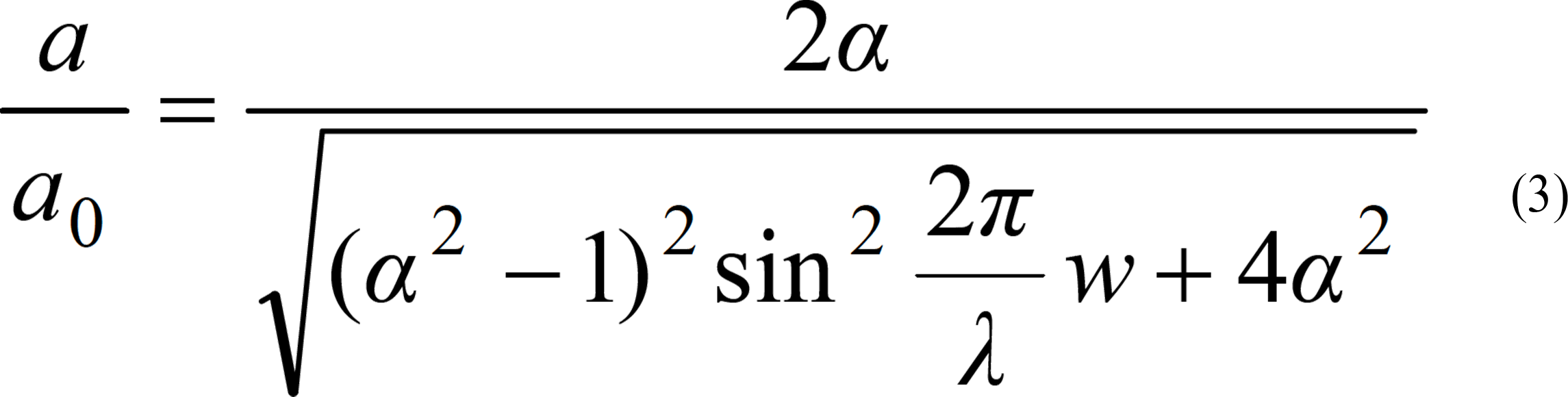
ここに,
a/a0 : 振動遮断壁前後の波動透過による加速度振幅比
α: 波動インピーダンス比(ρn Vn/ρn+i Vn+i)
ρi Vi: 波動透過モデルでの左側からの入射波に対する
右側媒質の波動インピーダンス
W: 媒質の厚さ (m)
f: 振動数 (Hz)
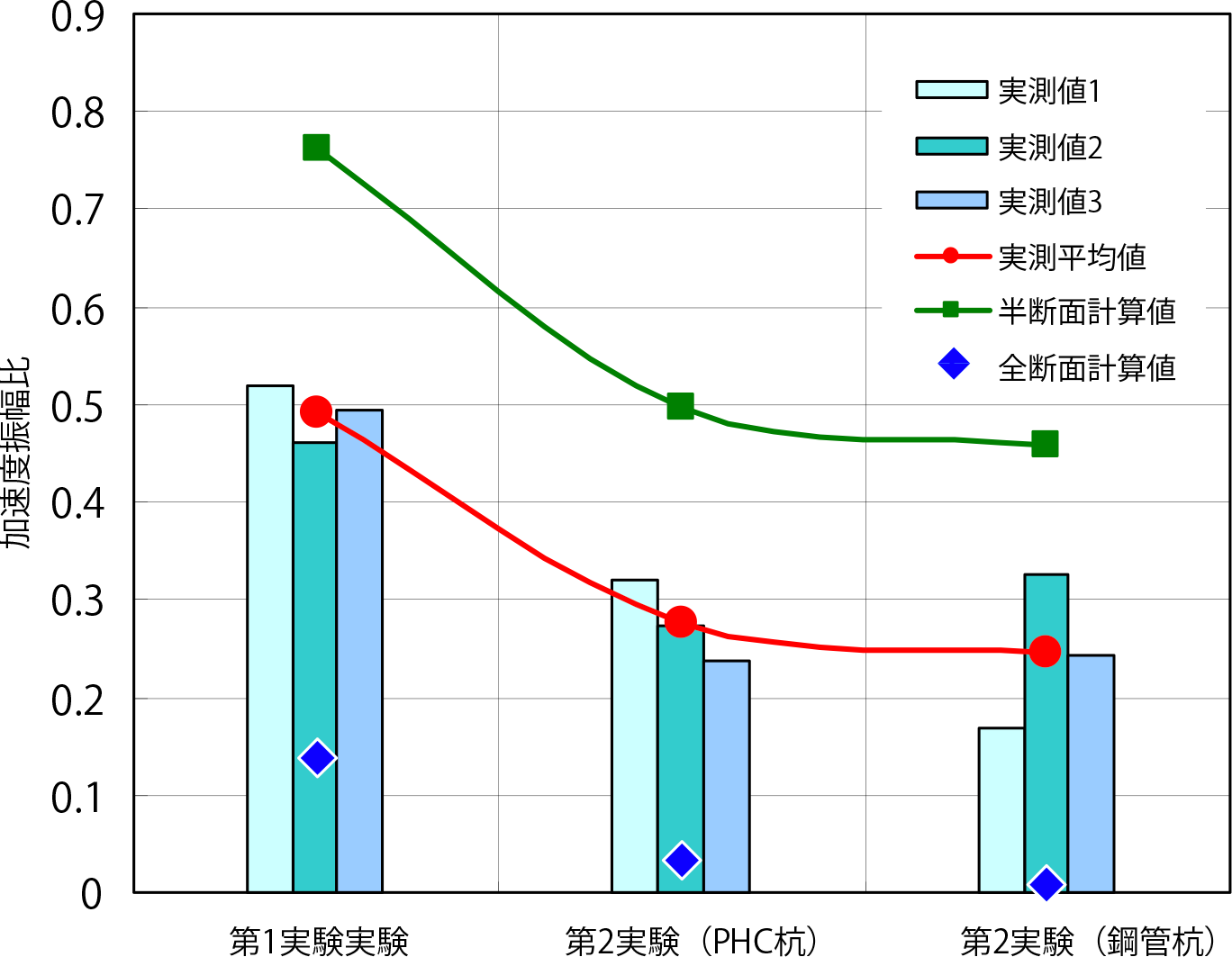
λ: 波長 V/f(伝播速度/振動数)(m)図-1916),17)は,本研究で対象としている第1実験および第2実験の波動透過モデルを示したものである,遮断壁は形状が円形であり,かつ遮断壁毎の接続方法が突合せによるものである.したがって,波動の進行方向に対して媒質が水平方向に一様な形状ではない.また,遮断効果は波動インピーダンス比と媒質の厚さによって支配されると考えられる.これらの項目を踏まえた上で,1本当りの半径部分の半断面をモデル化し,一様な断面と仮定して振動低減効果を検討している.図-20は,第1実験および第2実験(芯材:PHC杭),(芯材:鋼管杭)のケースにおける遮断壁の前面と背後の加速度振幅比の実測値と,図-19に示す波動透過モデルに対して式(3)で求めた計算値を示したものである.実測値は,遮断壁の中心ライン(実測値2として示す)と,その両サイド(実測値1,3として示す)の計測ラインでの値を示している.このグラフに示すように,半断面での計算値が実測値と比較して過大に評価されていることが分かる.参考として,全断面をモデル化したデータも図-20にプロットしている.この場合は,実測値に比較して過小評価となっている.このことから,振動低減効果は波動インピーダンス比による波動透過量の因子のみの影響で支配されないことが示唆される.しかしながら,その低減傾向は,計算値と実測平均値とでほぼ一致していることから,波動透過量が各遮断壁の振動低減傾向の支配的要因であることが分かる.したがって,図-14に示す第2実験においては,芯材が鋼管杭の場合にPHC杭に比べて振動低減効果が大きくなっており,波動透過量は鋼管杭の場合に小さいことが推察される.そこで,波動透過量以外の振動低減効果の因子としては,従来から使用されている鋼矢板やコンクリートによる地中遮断壁に比べて,本研究で用いている遮断壁はやわらかい弾性体を土と芯材の間に用いていることが挙げられる.一般に地盤が減衰性を有する場合,振動中の機械基礎から地盤に伝達される振動伝達率は,加速度振幅倍率を示す式(4)12)で表現される.本項では,この理論式を用いて,図-20に示す計算値が実測値の振動低減量より過小評価となる理由に関して考察した.
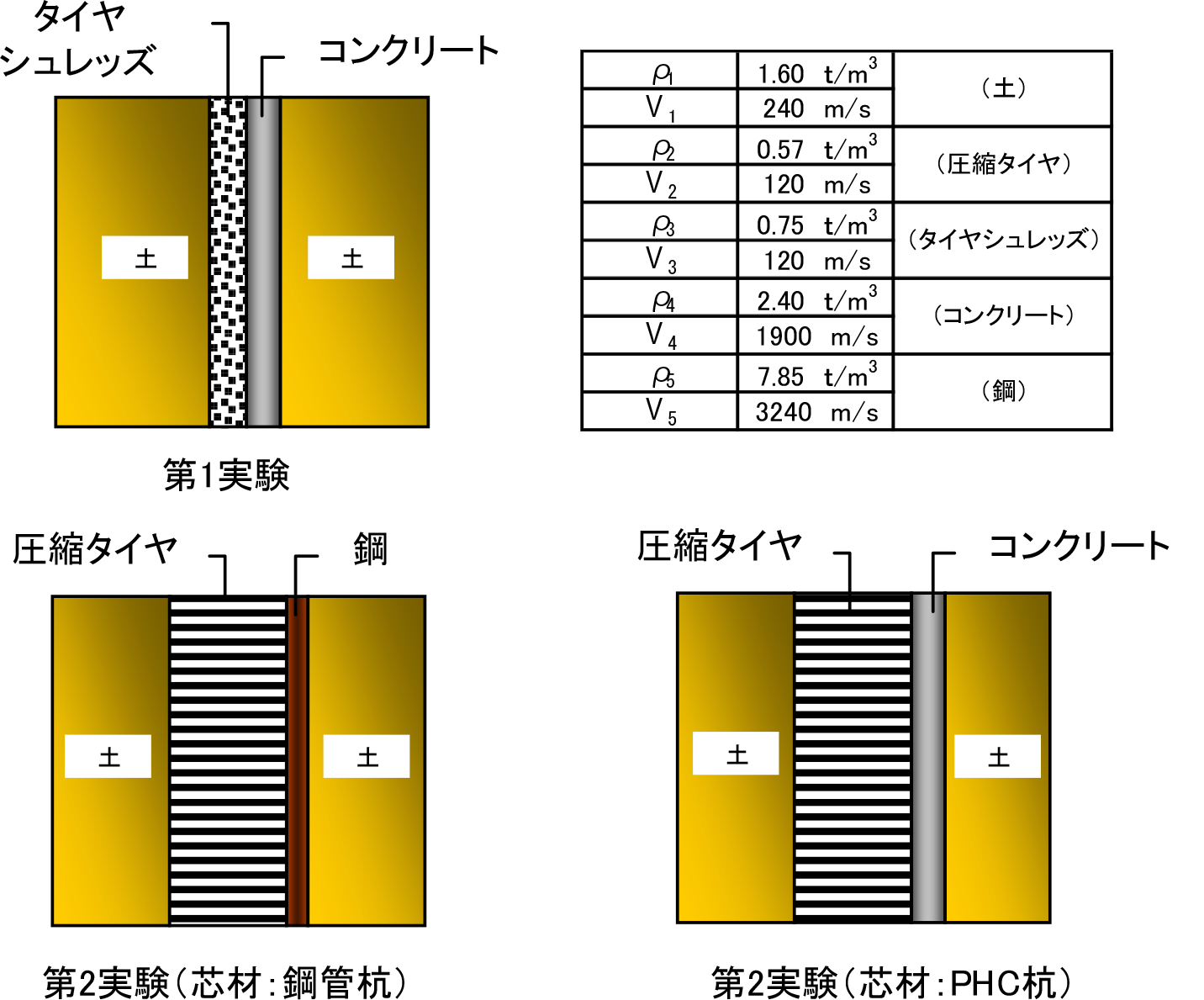
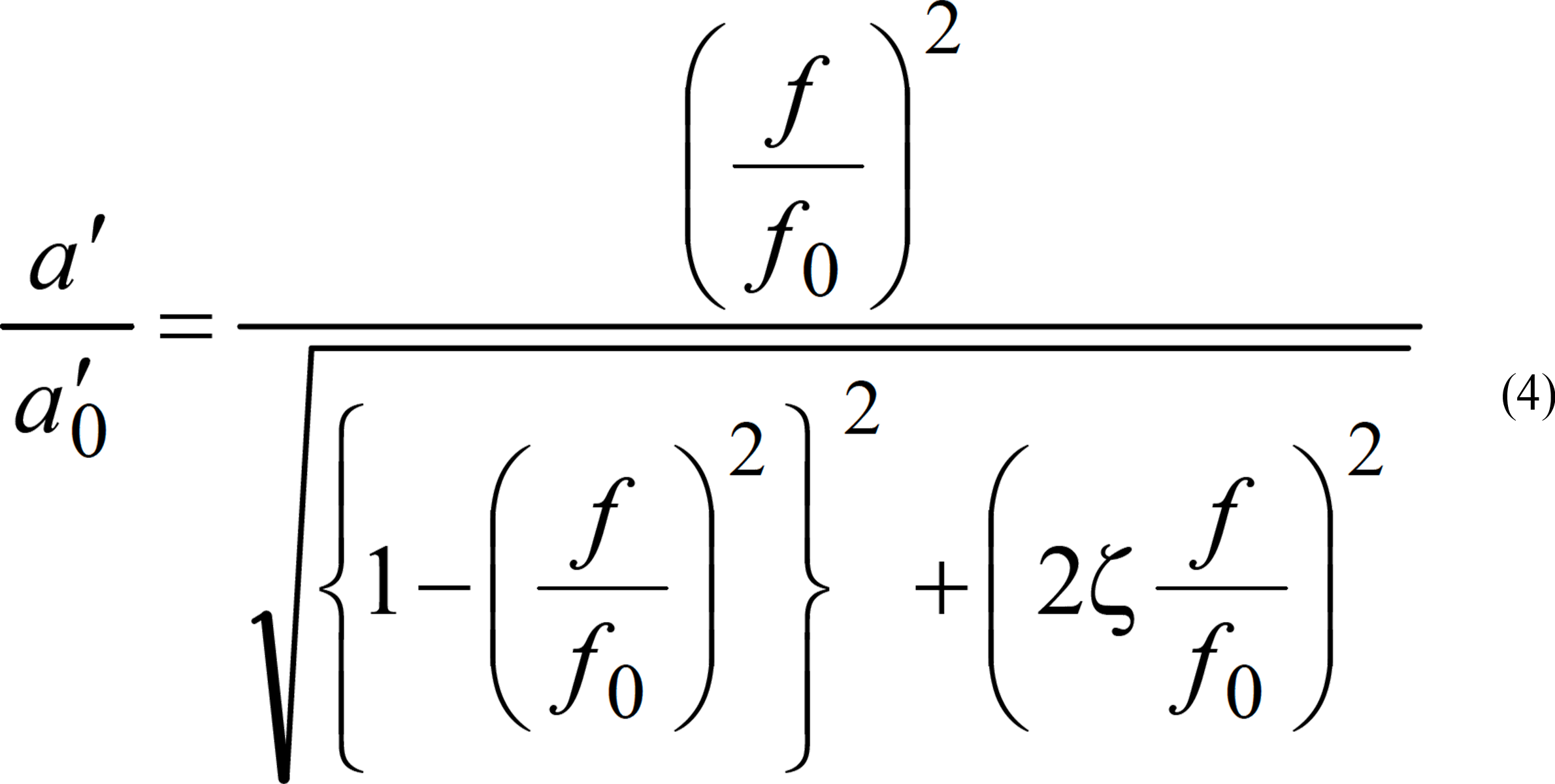
ここに,
a′/a′0: 振動遮断壁前後のバネ効果による加速度振幅比
f/f0: 振動遮断壁前後の振動数比
ζ: 減衰係数表-1には,第1実験および第2実験で得られた遮断壁の前面と背後の卓越振動数の実測値と減衰係数を示した.この減衰係数は,図-21に示す各遮断壁上部のピックアップで観測した加速度波形記録の赤丸で示した最大値および最大値から2 番目の値から,式(5)12)を用いて算出している.
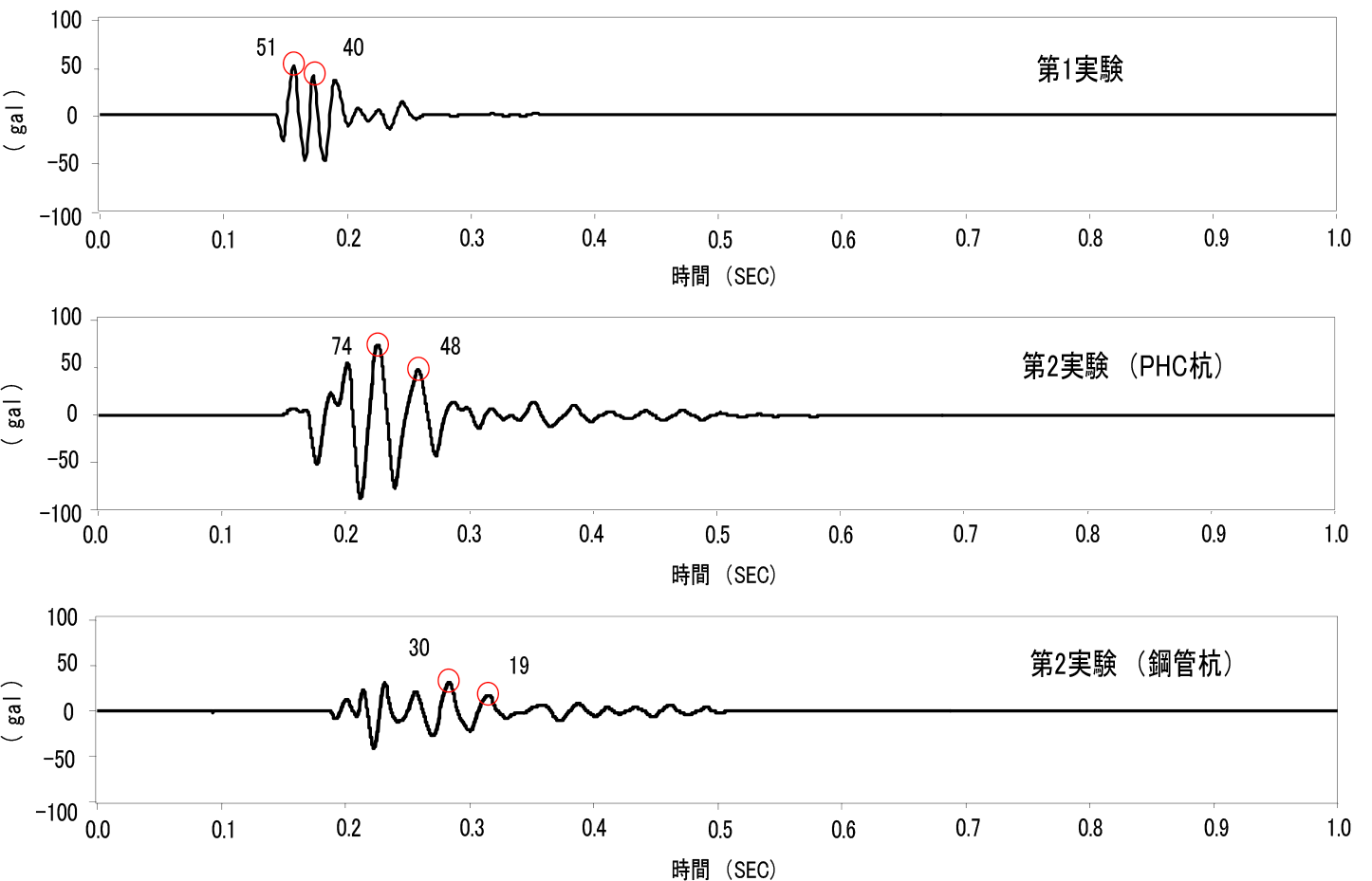
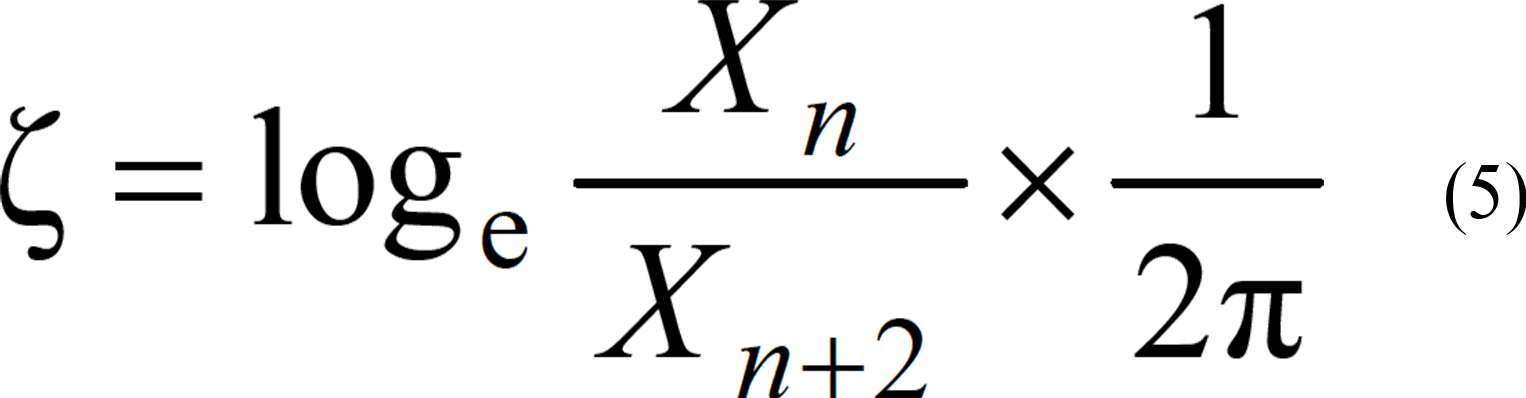
ここに,
ζ: 減衰係数
Xn: 加速度波形記録の最大値
Xn+2: 加速度波形記録の最大値から2番目の値表-1 振動数と減衰係数の一覧 第1実験 第2実験(PHC杭) 第2実験(鋼管杭) f (Hz) 36 23 26 f0 (Hz) 53 33 33 ζ 0.4 0.7 0.7 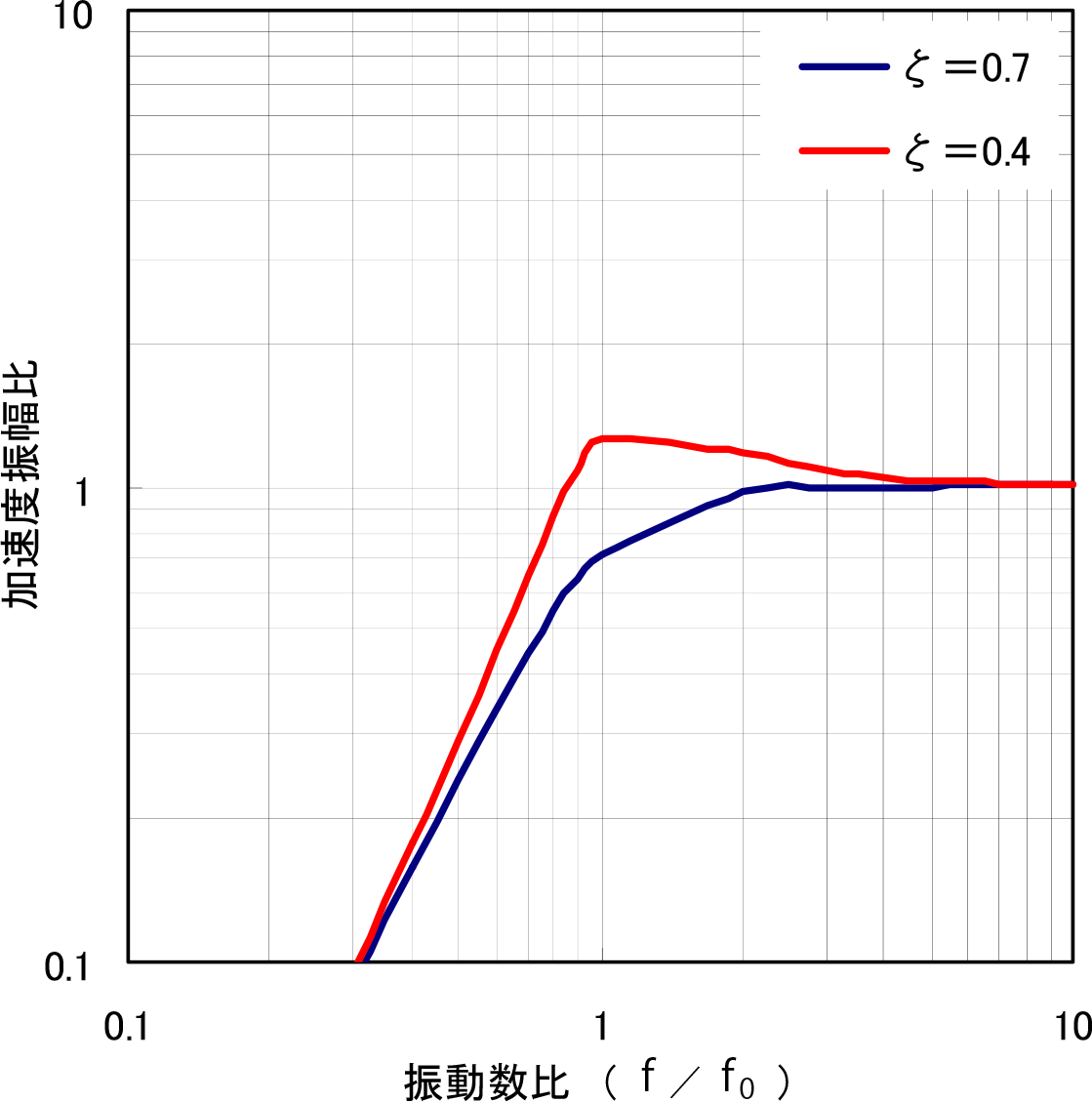
図-22は,減衰係数ζをパラメータとして式(4)の振動数比と加速度振幅比との関係を示したもので,ζ=0.4は第1実験に相当するものを表したものである.振動数比f/f0=1をピークに,それ以下の場合には加速度振幅比が著しく小さくなることを示している.また,ζ=0.7は第2実験に相当するものを表したもので,振動数比f/f0=2をピークに,それ以下の場合には加速度振幅比が著しく小さくなることを示している.この概念は,第2実験の結果が第1実験の結果に比べて振動低減傾向が大きくなる傾向と一致しているものと思われる.
表-1に示す第1実験と第2実験から得られた遮断壁の前面と背後の卓越振動数および減衰係数から,式(4)を用いてタイヤのバネ効果による加速度振幅比を求めた.この値に対して波動インピーダンス比から求めた加速度振幅比を式(6)で補正したものを図-23に示す.
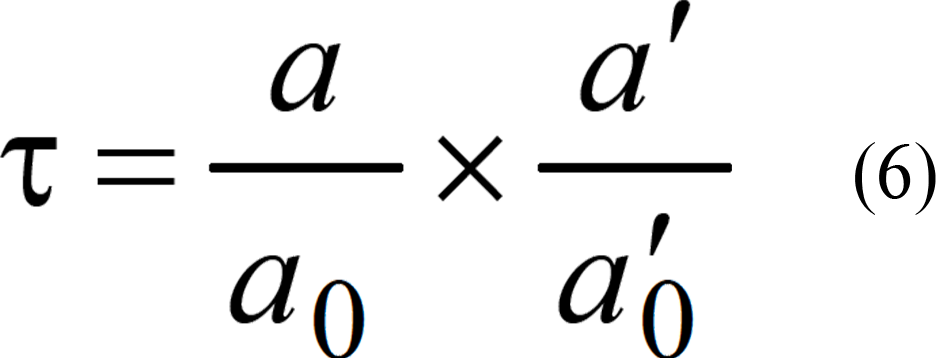
ここに,
τ: 振動遮断壁前後の加速度振幅比
a/a0: 振動遮断壁前後の波動透過による加速度振幅比
a′/a′0: 振動遮断壁前後のバネ効果による加速度振幅比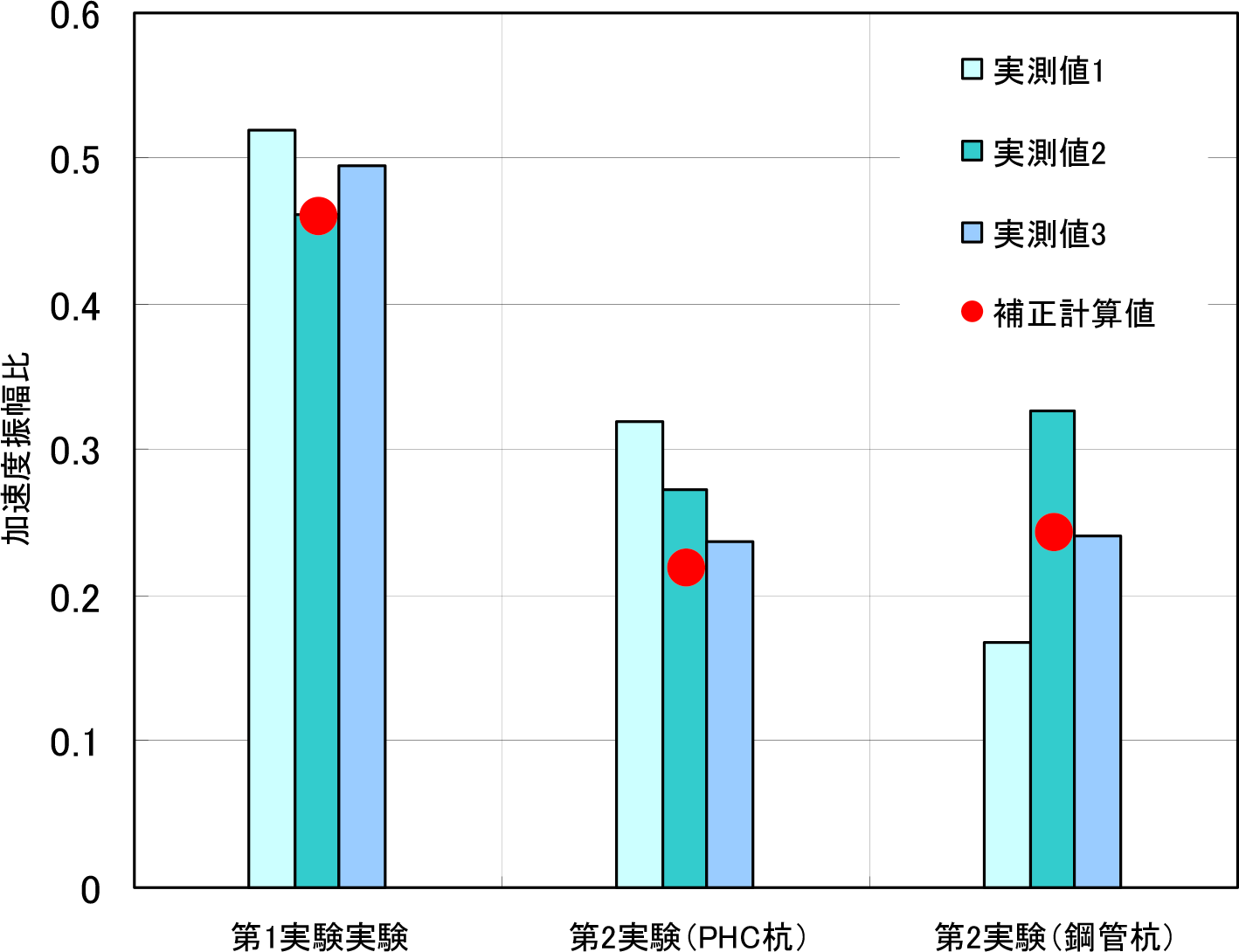
図-23は,第1実験および第2実験における振動遮断壁の前面と背後の加速度振幅比の実測値と,図-20に示した半断面モデルでの計算値の補正計算値を図示したもので,3ケースともに実測値がほぼ再現されていることが分かる.したがって,スクラップタイヤを用いた遮断壁の振動低減効果は,芯材部分のコンクリートおよび鋼による地盤との波動インピーダンス比に起因した波動透過による振動低減効果とタイヤのバネ効果による振動減衰効果との相互作用によって決定されているものと考えられる.
また,第1実験と第2実験との振動低減効果の差は,第1実験の波動透過モデルであるタイヤシュレッズとコンクリートとの組み合わせが,第2実験の圧縮タイヤと鋼およびコンクリートとの組み合わせと比較して,波動インピーダンス比が小さいことによっている.また,減衰係数も小さくなっているので,バネ効果も小さいためと考えられる.
本論文では振動低減効果の評価を振動遮断壁の前面と背後のみで行っている.遮断壁後方での評価については,EPS合成壁による地盤振動遮断効果とその評価法の提案において7),波動透過理論と距離減衰式および経路差を用いた評価により,遮断壁後方の振動低減効果を推定できることが分かっている.したがって,遮断壁後方での振動低減量の評価は,同様な手法により可能になるものと考えている.
-
-
数値シミュレーション解析による考察
前章においては,第1実験および第2実験での振動計測結果を基に,振動低減効果について2水準を比較して考察した.その結果,圧縮型遮断壁を用いた第2実験においては,原形型遮断壁を用いた第1実験と比較して大きな振動低減効果が得られることが確認できた.その振動低減メカニズムの解明をさらに検討するために,圧縮型遮断壁のPHC Typeを対象として,数値シミュレーション解析を実施した.
-
解析方法
地盤と圧縮型遮断壁を三次元的にモデル化し,地盤を強制加振して,地盤および圧縮型遮断壁の応答を算定した.地盤は薄層要素法を用いて成層地盤として層分割し,圧縮型遮断壁は三次元的有限要素でモデル化した.地盤応答は,薄層要素法による点加振解を用いて評価した.応答解析では,複素応答法を用いて線形解析するものとした.解析では,遮断壁前面の地盤を点加振で上下方向に強制加振して,各測定点での上下方向の加速度値を算定した.測定点は,図-10に示す遮断壁中心の測点2から6としている.地盤上に作用させる加振力は,加振点に最も近い測定点における加速度波形観測記録を再現するような加振力を逆算して求めている18).
-
解析モデル
実験フィールドおよび周辺のボーリング試験のデータから設定した地盤モデルを表-2に示す.なお,地盤のS波速度(VS)は,ボーリング試験のN値から式(1)を用いて算定した.また,P波速度(VP)は,GL-4.5mまでは地下水が無いために,地表面で計測した伝播速度を用いている,それ以深では地下水があるため,水のP波速度である1,500m/sと仮定している.
表-1 振動数と減衰係数の一覧 深度(m) 層厚(m) N値 ポアソン比 単位体積重量
(KN/m3)Vp(m/s) Vs(m/s) h(%) 0.00~-1.50 1.50 3 0.462 17.0 436 115 2.0 -1.50~-2.50 1.00 13 0.386 17.0 436 188 2.0 -2.50~-3.50 1.00 34 0.227 17.0 436 259 2.0 -3.50~-4.50 1.00 50 0.079 17.0 436 295 2.0 -4.50~-5.50 1.00 27 0.487 17.0 1500 240 2.0 -5.50~-6.50 1.00 30 0.486 17.0 1500 249 2.0 -6.50~-7.50 1.00 24 0.488 17.0 1500 231 2.0 -7.50~-8.50 1.00 31 0.486 17.0 1500 251 2.0 -8.50~-9.50 1.00 21 0.489 17.0 1500 221 2.0 -9.50~-10.50 1.00 14 0.492 17.0 1500 193 2.0 -10.50~-11.50 1.00 13 0.492 17.0 1500 188 2.0 -11.50~-12.50 1.00 20 0.489 17.0 1500 217 2.0 -12.50~-13.50 1.00 28 0.487 17.0 1500 243 2.0 -13.50~-14.50 1.00 21 0.489 17.0 1500 221 2.0 -14.50~-15.50 1.00 35 0.484 17.0 1500 262 2.0 -15.50~-16.50 1.00 16 0.491 17.0 1500 202 2.0 -16.50~-17.50 1.00 20 0.489 17.0 1500 217 2.0 -17.50~-18.50 1.00 21 0.489 17.0 1500 221 2.0 -18.50~-19.50 1.00 26 0.487 17.0 1500 237 2.0 -19.50~-20.50 1.00 30 0.486 17.0 1500 249 2.0 -20.50~ 49 0.480 17.0 1500 293 2.0 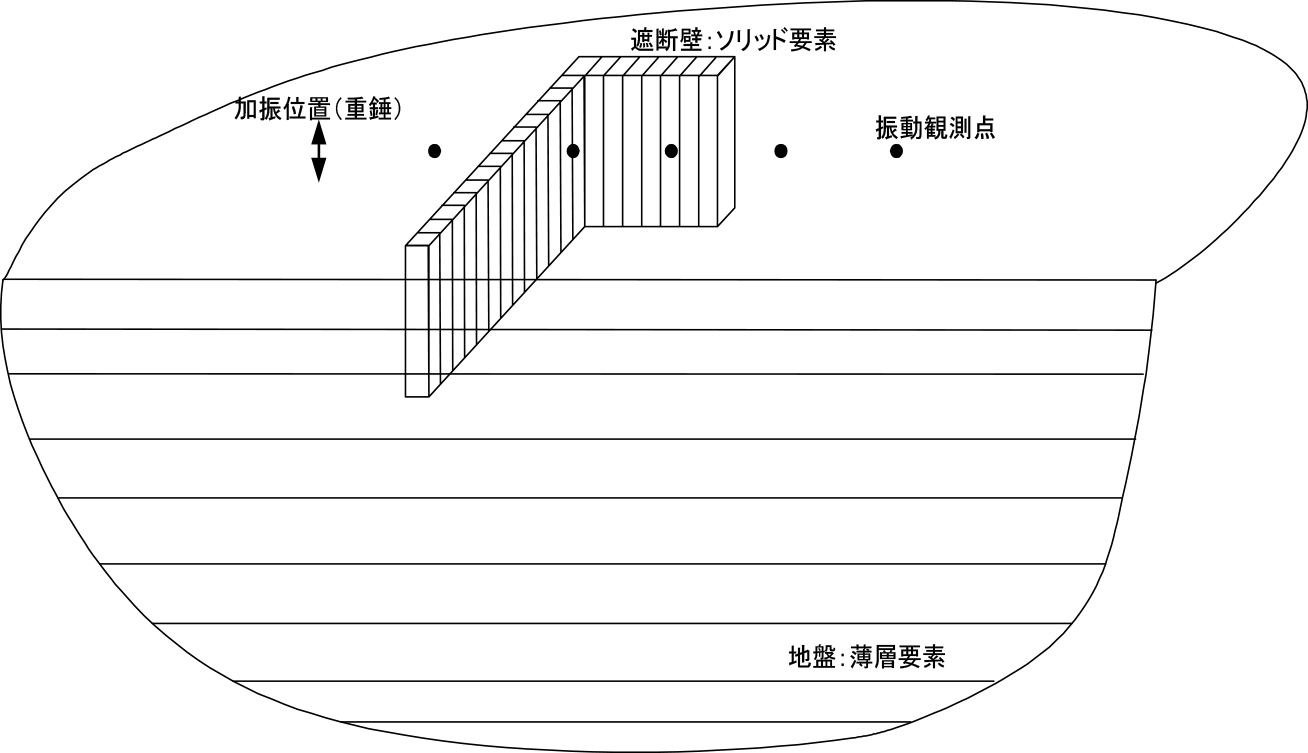
-
解析結果
振動加速度レベルの解析結果に1/3 オクターブバンド処理をして,実測値と解析値の中心周波数における周波数分布で比較した結果について述べる.
-
減衰係数による効果比較
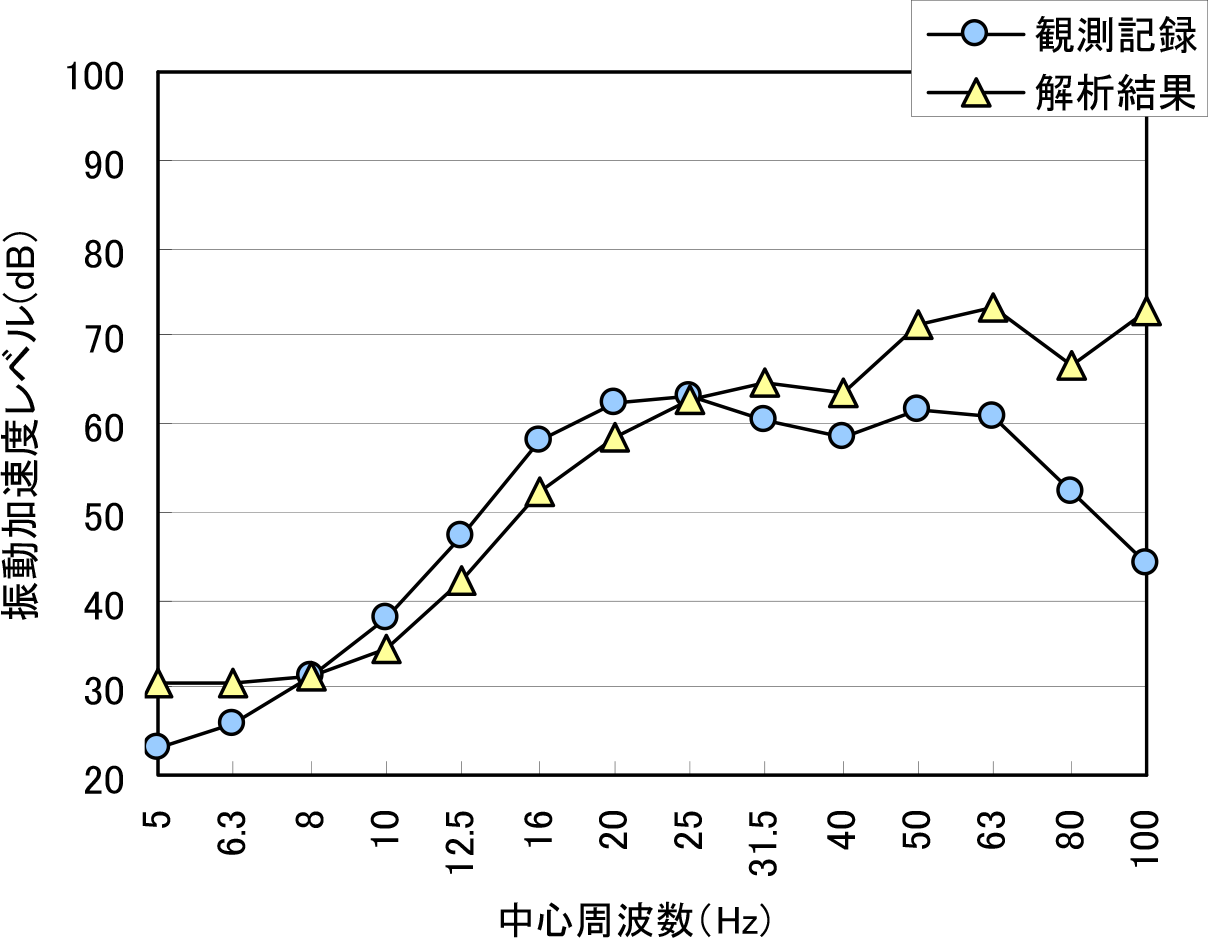
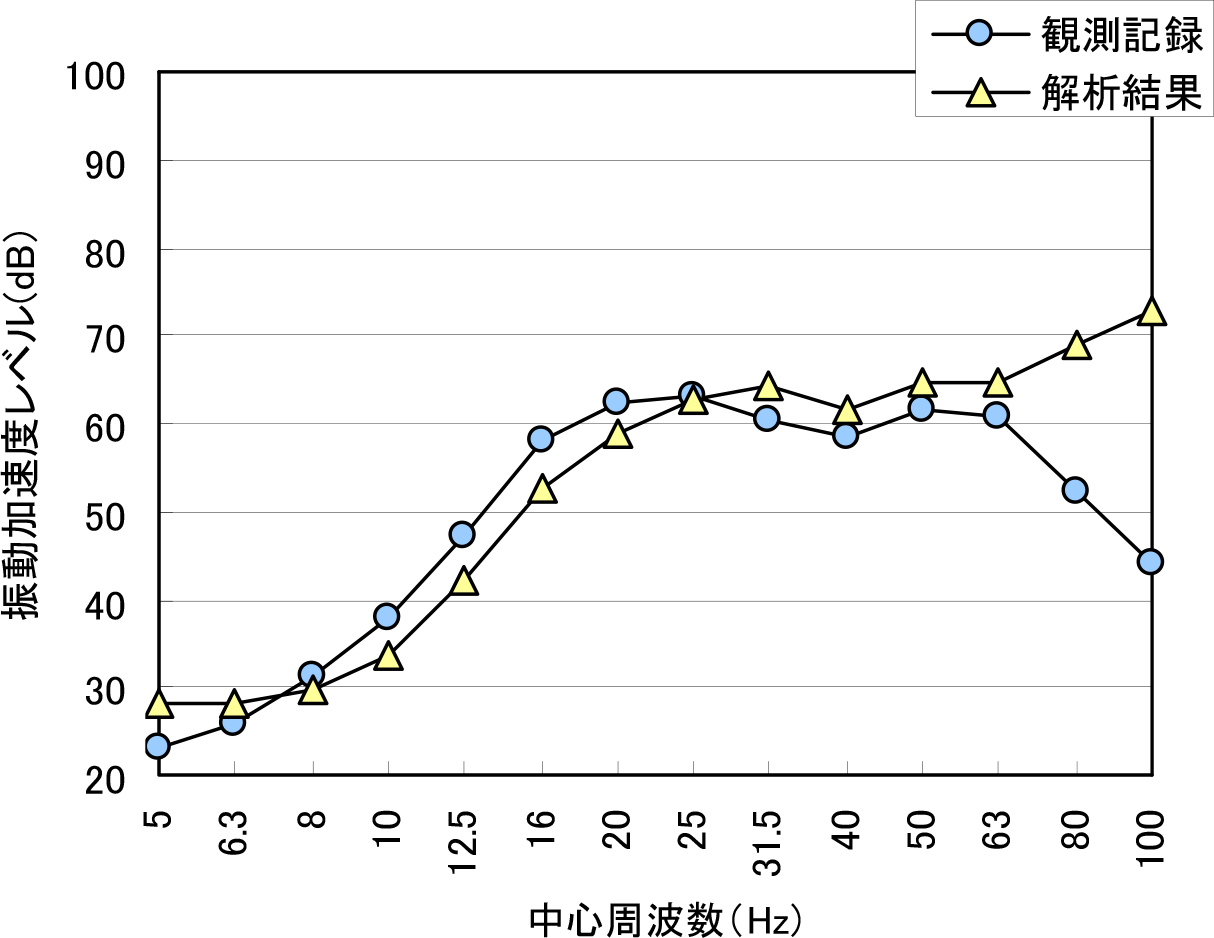
図-25,図-26には,圧縮型遮断壁に関して,遮断壁背後の解析値を遮断壁の減衰定数を3%とした場合と,10%とした場合の値について,実測値と比較して示している.図からも分かるように,減衰定数を3%とした場合,40Hz以上の周波数域が実測値に比較して表現されていないのに比べ,10%とした場合は63Hz以上の周波数域が表現できていないのみである.このことからも,減衰定数の増加に伴って解析値が実測値に近似することが分かる.したがって,減衰定数が振動加速度レベルの周波数分布に影響していることが示唆される.この傾向は,図-22に示した減衰係数をパラメータとした加速度振幅比との関係と符合しているものと考えられる.
-
等価質量による効果比較
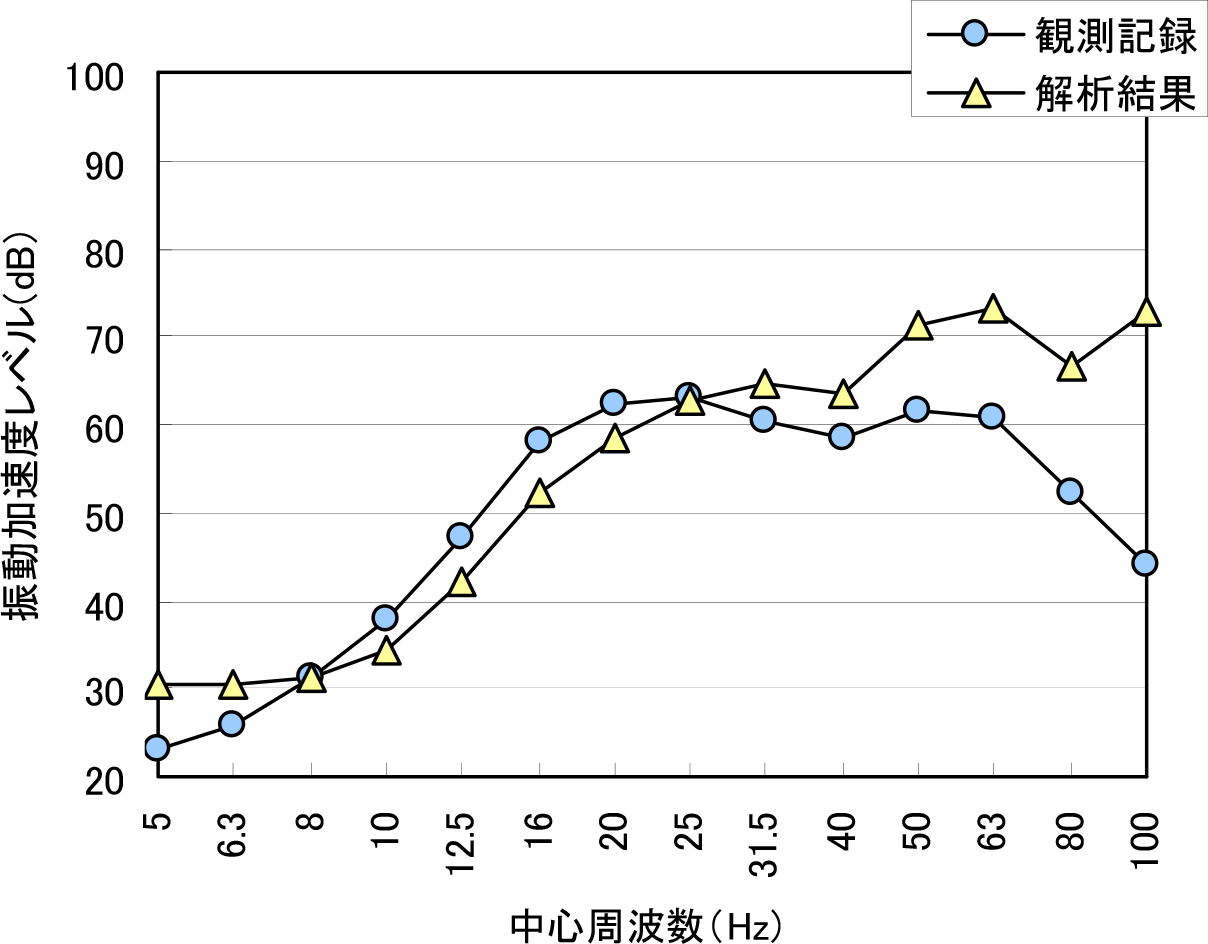
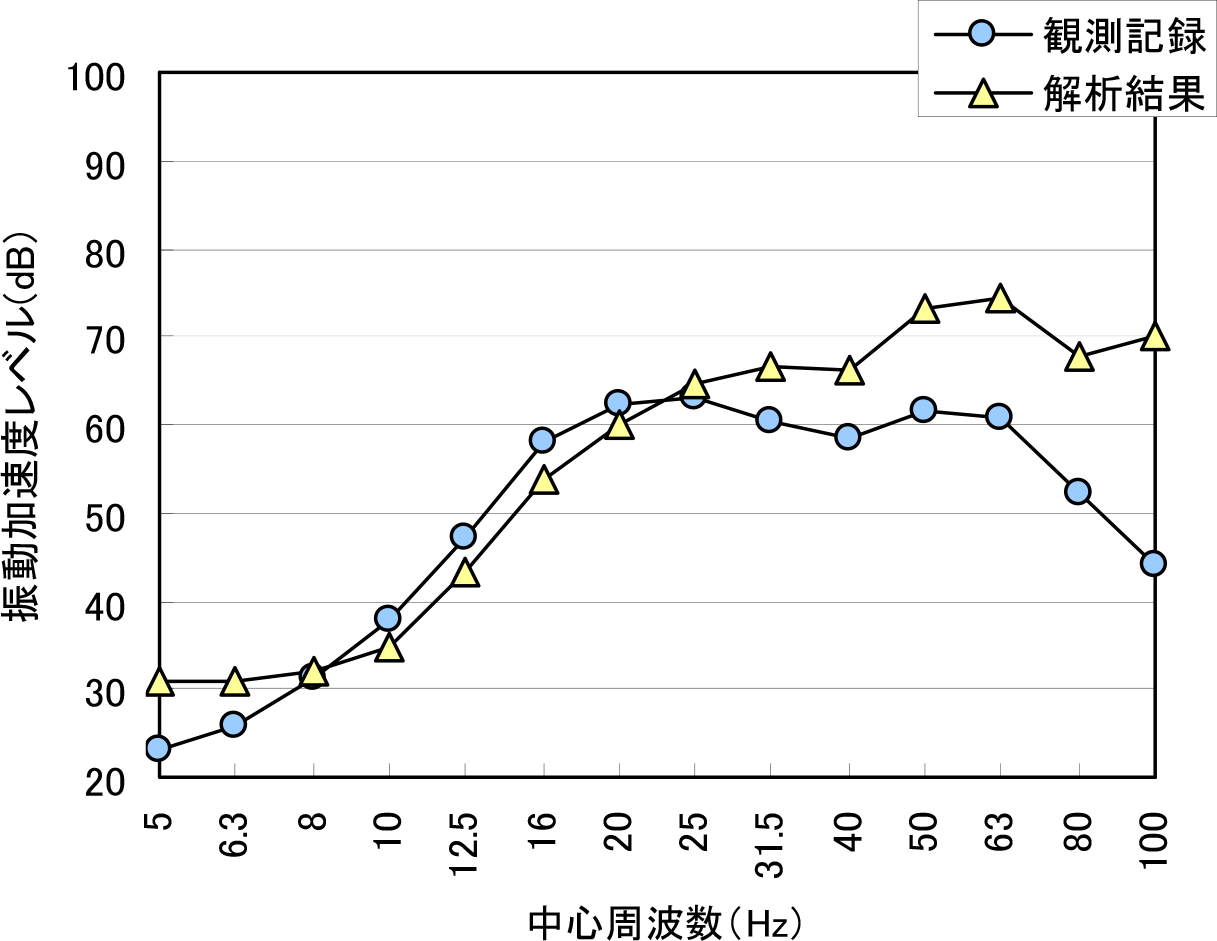
図-27,図-28は,圧縮型遮断壁の等価質量とその4倍の質量とした場合の解析値と実測値を示したもので,PHC Typeの一本当りの等価質量を0.7m×0.7m×3mの四角柱と仮定して,単位質量を620kg/m3としている.図から分かるように,両者ともに25Hz以上の周波数域において実測値に比べて過大評価となっている.しかし,卓越周波数部分である23Hz付近では,両者ともに良く対応していることが分かる.また,8Hzから25Hzまでの周波数域に着目すると,等価質量を4倍とした場合に実測値と解析値が良く対応していることが分かる.これは,上述の5.(2)で述べた波動透過理論による加速度振幅比の傾向で,第1実験よりも第2実験の質量が大きいことによる,波動インピーダンス比が大きく得られた考察に一致していると考えられる.しかしながら,25Hz以上の周波数域では差異が認められる.これは,本解析手法では,地盤と遮断壁とが一体化して挙動しているかどうかなどの遮断壁の挙動を十分に解明し得ていないことによるものと考えられる.したがって,今後の検討においては,この点を考慮した評価も必要であると考えている.
-
-
-
結論
本論文では,スクラップタイヤを用いた原形型遮断壁および圧縮型遮断壁による地盤振動に関して,伝播経路対策工としての振動低減特性を比較・検討するために,実物大フィールド実験結果と数値シュミレーション解析によりその振動低減効果を考察した.
本研究で得られた結果をまとめると,以下の通りである.
- 原形型遮断壁を用いた実物大の第1実験においては,加振入力を重錘落下および重機走行加振として自然地盤での計算値と比較した.その結果,両加振条件ともに加振点から3.5m~4.0m地点(遮断壁裏面)で3dB~4dB程度の振動低減量を示した.また,遮断壁により特に顕著な振動低減効果が得られる周波数範囲は,重錘加振で40Hz~60Hz,重機加振で45Hz~75Hzである.
- 圧縮型遮断壁を用いた実物大の第2実験では,加振入力を重錘落下とし,遮断壁の中心部の芯材をPHC杭および鋼管杭として遮断壁の振動低減効果を自然地盤の結果と比較した.PHC Typeの遮断壁では,加振点から4.75m~16.0m地点の遮断壁後方では,5dB~10dB程度の振動低減量を示した.また,鋼管Typeの遮断壁では,加振点から4.75m~16.0m地点の遮断壁の後方では,7dB~12dB程度の振動低減量を示した.加速度スペクトルから評価すると,振動低減効果が得られる周波数範囲は23Hz~70Hzであった.
- 第1実験と第2実験での結果を,遮断壁の埋設深さを波長で除した値と遮断壁の前面と背後の加速度振幅比との関係から評価すると,第2実験のものが第1実験のものに比べて振動低減効果が大きく得られる.また,第2実験の結果は,空溝の振動低減効果量に近似した値を示す.
- 遮断壁の振動低減効果の評価に関しては,波動透過理論と地盤に減衰性のバネを介した場合の加速度振幅倍率式を用いて補正することにより,実測値をほぼ再現できる.したがって,スクラップタイヤを用いた遮断壁の振動低減効果は,芯材部分であるコンクリートおよび鋼管と地盤との波動インピーダンス比に起因する波動透過現象による振動低減効果とタイヤのバネ効果による振動減衰効果との相互作用によって得られたものと考えられる.
- 数値シュミレーション解析においては,圧縮型遮断壁の減衰定数の増加に伴って実測値への近似度合いが増加する.したがって,減衰定数の変化が振動加速度レベルの周波数分布に影響していることが示唆された.また,等価質量を4倍とした場合に25Hz以下での実測値と解析値が良く対応していることから,遮断壁の質量も遮断効果に関係していることが示唆された.
参考文献
- 社団法人土木学会: 土木用語大辞典, pp. 1278-1279, 1999.
- JATMA: タイヤリサイクルハンドブック, リサイクル状況, 2000.
- JATMA: 日本のタイヤ産業, 2004.
- 小倉一利, 矢島寿一, アショカ・K・カルモカル: タイヤチップスの強度・変形特性, 第41 回地盤工学研究発表会講演集, pp. 585-586, 2006.
- 御手洗義夫, 安原一哉, 菊池喜昭, 大谷 順, Ashoke K Karmokar: タイヤチップ混合固化処理土の変形・透水特性, 第41回地盤工学研究発表会講演集, pp. 599-600, 2006.
- 社団法人土木学会関西支部: 「都市域における環境振動の実態と対策講習会」テキスト, pp. 107-108, 2005.
- 早川 清, 中谷郁夫, 緒方広泰, 前 育弘: EPS 合成壁による地盤振動遮断効果とその評価法の提案, 土木学会論文集, Vol. 63, No. 2, pp. 138-148, 2007.
- 櫛原信二, 野津光夫, 日置和昭: ガスクッションを用いたハイブリット遮断壁の鋼矢板仕様に関する一考察, 第41回地盤工学研究発表会講演集, pp. 2391-2392, 2006.
- Massarsch, K. R. : Vibration Isolation using Gas-Filled Cushions, Soil Dynamics Symposium to Honor Prof. Richard D. Woods, Geofrontiers 2005, pp. 24-26, 2005.
- 早川 清, 樫本孝彦, 森脇昌一: 環境に配慮した廃タイヤ振動防止対策法, 物理探査, 第58 巻, 第4 号, pp. 391-396, 2005.
- 社団法人地盤工学会: 地盤・基礎構造物の耐震設計, 地盤工学・実務シリーズ13, pp. 78-79, 2001.
- 経済産業省産業技術環境局: 公害防止の技術と法規〔振動編〕, pp. 68-69, pp. 84-85, 1996.
- Richart, F. E. Jr. , Woods, R. D. and Hall, J. R. Jr. : 土と基礎の振動, pp. 92-93, pp. 288-289, 鹿島出版会, 1975.
- 吉川 実, 前原 博, 幸左堅二, 吉川正昭: 橋脚および地盤の模型振動実験(中), 橋梁と基礎, 85-2, pp. 39-40, 1985.
- 江島 淳: 地盤振動と対策, pp. 183-184, 集文社, 1979.
- 自然科学研究機構国立天文台: 理科年表, pp. 418-419, 2007. 60 土木学会論文集G Vol. 64 No. 1, 46-61, 2008. 2
- 中谷郁夫, 神村洋介, 早川 清: EPS 合成壁による振動低減挙動の計測処理と低減効果の評価法に関する提案, 「地盤工学会関西支部 地盤の環境・計測技術に関するシンポジウム論文集」, pp. 77-82, 2006.
- 早川 清, 原 文人, 植野修昌, 西村忠典, 庄司正弘: 鋼矢板による地盤振動の遮断効果と増幅現象の解明, 土木学会論文集, Vol. 62, No. 3, pp. 492-501, 2006.





